10. Fortsetzung RUBATO
- MeloRUBETTE
- HarmoRUBETTE
- Interpretation: PerformanceRUBETTE
Als zweite Analyse-Rubette wollen wir die MeloRUBETTE diskutieren. Sie bringt gegenüber der MetroRUBETTE einige theoretische, aber auch praktische Probleme mit betreffend den Rechenaufwand
Wir werden im Anschluss eine Übersicht geben zur PerformanceRUBETTE, damit man auch die Anwendung der anlytischen Rubetten erkennen kann.
Wir werden aber die HarmoRUBETTE nur kurz besprechen können, denn sie sehr kompliziert zu erklären, da man die Riemannsche Funktionstheorie und einige Problemstellungen aus der Harmonielehre genauer diskutieren müsste.
Die MeloRUBETTE
Um die Beschreibungsebene etwas zu vereinfachen, trotzdem aber die wesentlichen Punkte beibehaltend, werden wir hier nur von einer Sorte von Noten sprechen, nämlich Denotatoren der Form
EHNote:.Product(E,H);
mit der Form E:.Simple(R) für Einsatzzeit und H:.Simple(R) für Tonhöhe.
Ein Motiv ist dann ein Denotator in der Form Loc:.Powerset(EHNote), also eine lokale Komposition M = {N1,N2,...,Nk} von Noten in EHNote. Dabei stellen wir die Bedingung, dass die Projektion
p_E : M --> M_E
welche jeder Note Ni in einem Motiv M ihre Einsatzzeit E Ni und damit die lokale Komposition
M_E = p_E(M)={E_N1 , E_N2 ,...,E_Nk}
in E zuordnet, eine Bijektion p_E: M --> M_E definiert. Das heisst: Zwei Noten sind verschieden genau dann, wenn ihre Einsatzzeiten verschieden sind, keine Akkorde oder Intervalle simultaner Noten, siehe Bild 97!
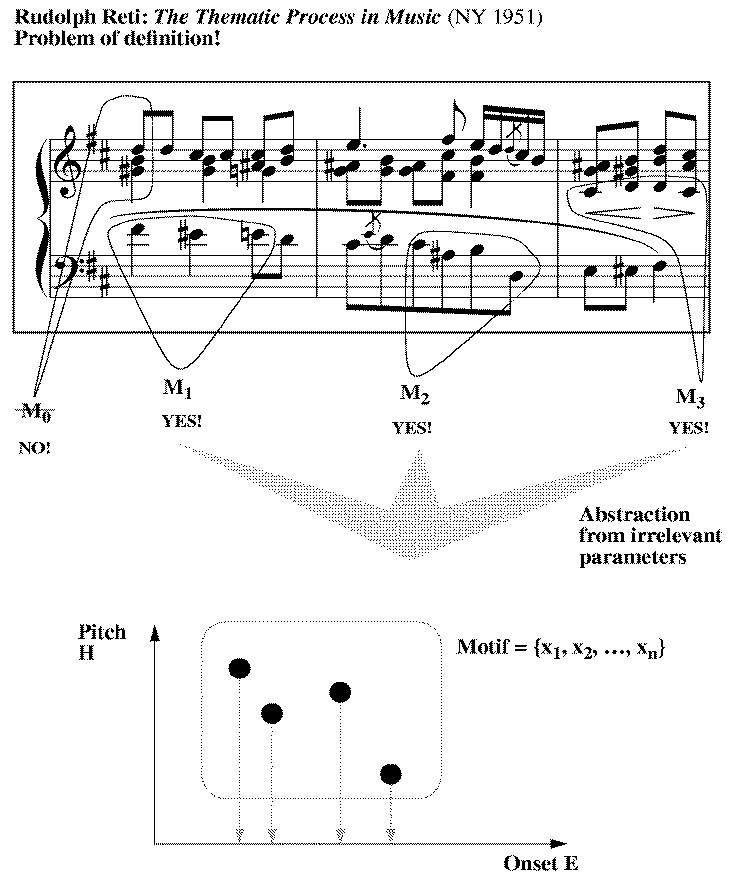
Bild 97: Motive der Form EHNote und bijektive Projektion auf E
Wir stiften in Bild 97 auch einen Bezug zu Rudolph Retis bekanntem Werk über den thematischen Prozess in der Musik. Der Bezug ist daher angebracht, weil in der Musikwissenschaft der Begriff des Motivs und der motivischen Analyse noch weitgehend kontrovers resp. inexistent sind. Reti weigert sich in genanntem Buch gar, nach einem provisorischen Versuch einer Definition der Terms "theme", eine genaue Definition des Begriffs des Themas zu geben (Op. cit., p. 12, Fussnote):
| In general, the author does not believe in the possibility or even desirability of enforcing strict musical definitions. Musical phenomena come to existence in the constant fluence and motion of compositional creation. Therefore any description of theme must finally prove but approximations. |
Bezogen auf diese Strukturen von Motiven soll die MeloRUBETTE Gewichte von Noten in EHNote ermitteln.
Wir wollen gewissermassen so ein Gewicht als Aussage darüber erhalten, was die Relevanz einer Note im motivischen Kontext eines Musikstücks sein kann.
Eine einfachere Frage kann man gleich vorweg lösen: Wenn man weiss, was das Gewicht weight_A(M) von Motiven M in der gegebenen Komposition ist unter einer bestimmten Motivanalyse A, was ist dann ein gutes Mass für das Gewicht einer Note Ni? Man kann das Gewicht einer Note Ni in dieser Komposition definieren als
| weight_A(Ni) = Σ_{Motiv M enthält die Note Ni} weight_A(M) |
also die Summe der Gewichte aller betrachteten Motive zu dieser Kompsition, die Ni als Note enthalten.
Die Kernfrage wäre also: Was also ist das Gewicht eines Motivs?
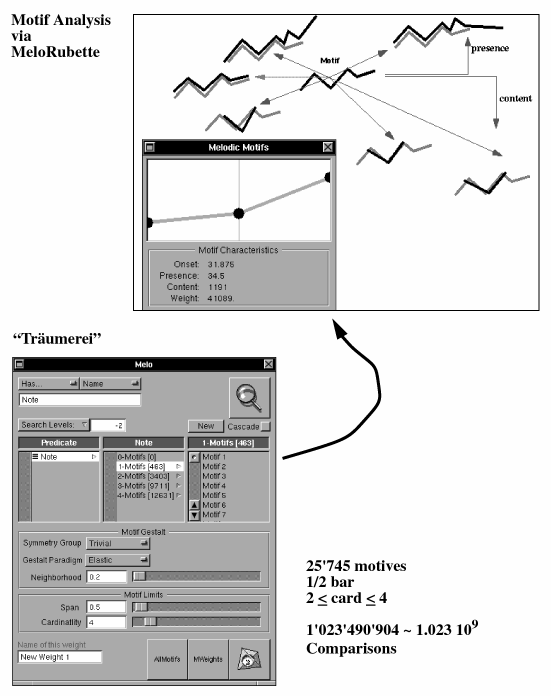
Bild 98: Motiv-Analyse mit der MeloRUBETTE
Wir gehen so vor (siehe auch Bild 98, untere Hälfte, Hauptfenster MeloRUBETTE): Man wählt zunächst in einer Komposition alle Motive aus, die in gewissen Grenzen liegen. Wir können auf der MeloRUBETTE folgende Grenzen festlegen:
- Card = maximal zugelassene Anzahl Töne in einem Motiv
- Span = maximaler Abstand zwischen der Einsatzzeit des ersten und derjenigen des letzten Tones eines Motivs
Dies stellt man im Hauptfenster unten ein. Die Liste aller Motive wird dann aus der gegebenen Komposition, in Bild 98 die Träumerei, erstellt. Die einzelnen Motive können aus dem Browser (Bild 98, Hauptfenster, Mitte) ausgewählt und im kleinen Fenster (Bild 98, Hauptfenster, oben) eingesehen werden.
Als nächstes wählt man ein "Gestaltparadigma" für Motive aus. Damit entscheidet man sich dafür, was für Eigenschaften eines Motivs für den Vergleich von Motiven gleicher Grösse wesentlich sein sollen. Bei der Einstellung "Dia" (=diastematischer Index) betrachtet man nur die Information, ob sukzessive Töne des Motivs steigen, fallen oder gleich hoch bleiben. Damit reduziert sich die Information auf eine Reihe von +1 (Steigen), -1 (Fallen) oder 0 (gleich bleiben). Das Gestaltparadigma "Elastic" behält von einem Motiv die Steigungswinkel der sukzessiven Töne (in der EH-Ebene) sowie das Verhältnis sukzessiver Seitenlängen von Intervallen sukzessiver Töne, siehe Bild 99. Die Einstellung des Gestalttypus geschieht im Hauptfenster unter "Gestalt Paradigm".

Bild 99: Diastematischer Index und elastische Gestalts
Nun stellt man noch ein, wie viel die Gestalten von Motiven verschieden sein dürfen, damit wir sie als "ähnlich" zulassen. Man kann das im Sinne eines "Abstandes" dieser Gestalten präzise machen. Wie diese Grenze ("Neighborhood" auf der MeloRUBETTE, Bild 98, Hauptfenster, unter dem Browser). Was man einstellt als Neighborhood, ist natürlich nicht das Problem der Software, sondern unseres, also ein möglicherweise psychologisch motiviertes, so dass wir im Rahmen der Aufgabenstellung die Grenzen unter dem Feld "Neighborhood" (Bild 98) einzugeben haben.
Die Software kann jetzt beim Vergleich zweier Motive, die gleich viele Töne haben, entscheiden, ob sie "ähnlich" sind oder nicht: Sie sind "ähnlich", wenn ihr Abstand kleiner ist als die gewählte Zahl "Neighborhood". Um nun weiter das Gewicht eines Motivs zu bestimmen, werden zwei Hilfsgrössen ausgerechnet: die Präsenz und der Inhalt eines Motivs M (siehe wieder Bild 98, rechts oben).
Präsenz: Wir betrachten alle Motive N in unserem Inventar, welche mindestens so viele Töne haben wie das gegebene Motiv M, und die Teilmotive M* enthalten (deren Töne aber nicht notwendig aufeinander-folgend sein müssen in N), die ähnlich sind zu M. Wir zählen die Zahl dieser Situationen und nennen das Resultat Präsenz presence(M) von M. Wir erfahren so, an wievielen Motiven M -- bis auf Æhnlichkeit -- beteiligt ist.
Inhalt: Wir betrachten alle kleineren Motive N in unserem Inventar, die zu einem Teilmotiv M* von M ähnlich sind und zählen diese Fälle. Das wird Inhalt content(M) von M genannt. Wir erfahren so, wieviele Motive sich "unter" M einfinden.
Es ist nun vernünftig,
| weight_A(M) = presence(M) x content(M) |
zu definieren, wobei die Analyse A nun alle Parameter, die wir oben betrachtet haben, einschliesst: Gestaltparadigma, Card, Span, Æhnlichkeit. Bild 98 zeigt die Situation für die Träumerei mit den angegebenen (engen!) Grenzen, und man sieht die enorme Rechenleistung für Motivvergleiche, welche schon mit den wenigen (463) Tönen der Träumerei zu erbringen sind. Es sind bei der engen Grenze von Card = 4 (also nur Motivchen von 2, 3 und 4 Tönen!) und Span = 1/2 Takt doch schon 25'745 Motive. Und die Software muss jetzt rund 1 Milliarde Vergleiche bezüglich Æhnlichkeit anstellen.
Bemerkung: Es kann mit der Einstellung "Symmetry Group" auch ein Gestaltvergleich mit der Umkehrung, dem Krebs oder der Krebsumkehrung des Vergleichsmotivs angestellt werden.
Diese Rubette stellt uns vor zwei Probleme:
1. Problem:
Wie kann man eine überbordenede Kombinatorik in den Griff bekommen?
Welche sind die Lösungsmethoden? Dies hier die Workarounds:
- Statistik (insbesondere: neuronale Netze)
- schnellere Maschinen
- bessere Algorithmen
Die Lösung muss von Fall zu Fall überlegt und verfolgt werden. Die Wege 2 und 3 sind scheinbar gut, führen aber nicht zu Lösungen, die qualitativ besser sind. Wenn man normale Musikstücke, etwa von der Grösse eines Sonatenhauptsatzes, nimmt, nützen alle diese Methoden nichts. Mehr kann man sich von Statistik versprechen: Man muss Stichproben unter den Motiven machen, um die grossen Zahlen im Rahmen des Möglichen zu halten.
2. Problem:
Wir haben jetzt eine Gewichtsfunktion weight_A : EventSet --> R, die aber auf den Noten des EventSets im zweidimensionalen EH-Raum definiert ist. Wir kann man nun interpolieren, um gleich wie beim metrischen Gewicht eine Gewichtsfunktion auch zwischen den Events zu erhalten. Auch hier ist die Spline-Theorie anzuwenden, und wir haben das auch in den diversen Rubetten so gemacht.
Wir können also davon ausgehen, dass alle Gewichte immer auf natürliche Weise auf alle zwischen den Noten des EventSet liegenden Punkte ausgedehnt worden sind. Hier zwei Beispiele, die wir in der Vorlesung kommentieren.
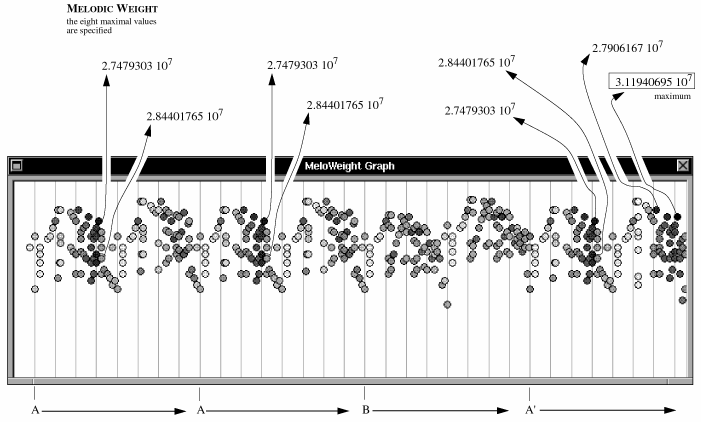
Bild 100: Bild von melodischem Gewicht zur Träumerei mit Kreisscheiben
Bild 100 zeigt die Gewichte der EH-Noten in der Träumerei als grauwertige Kreisscheiben, deren Dunkelheit proportional zum Gewicht ist.

Bild 101: Bild von Spline-erweitertem melodischem Gewicht der ersten 8 Takte der Träumerei
Bild 101 zeigt die Gewichte der EH-Noten in den ersten 8 Takte der Träumerei durch Splines interpoliert, hier gibt die Dunkelheit der Landschaft die Höhe des Gewichts.
| Achtung: In der Musikwissenschaft wird man Motive als "semantisch geladene" Tongruppen auffassen, es ist also nicht jedes Motiv in unserem Sinne in der Musikwissenschaft ein Motiv. |
Unser Vorgehen war hier, die Semantik, also die Bedeutung, die einem Motiv innewohnt, durch die Gewichtsfunktionen zu konstruieren. Wir vergleichen jedes Motiv mit jeden anderen und erhalten so via Präsenz und Inhalt durch sein Gewicht seine Bedeutung, die es im gegebenen Inventar des ausgewählten Musikstücks hat. Damit wird Retis Forderung nach einer immanenten Konstruktion der Motivik nachgegangen (s. dazu auch Kopfermanns interessanter Kommentar p. 297 zu Reti). Wie weit sie so erfüllt oder angenähert worden ist, muss die weitere Diskussion erweisen.
Die HarmoRUBETTE
Die HarmoRUBETTE ist unter den analytischen Rubetten die weitaus komplizierteste und auch vom Rechenaufwand her die komplexeste. Wir geben hier lediglich eine Übersicht.
Wie schon in den vorangehenden Diskussionen der musikwissenschaftlichen Situation ist auch in der Harmonielehre eine theoretische Unsicherheit vorhanden, so etwa in dem bekannten Zitat von Carl Dahlhaus zu Hugo Riemanns Harmonielehre (siehe Referenz in "The Topos of Music", p.819):
Eine Theorie aber, die gerade dort versagt, wo das Phänommen, das sie erklären soll,
ins Vage und Unbestimmte gerät, darf als adäquat gelten. |
Die Idee dieser Rubette ist eine Implementierung der Riemannschen Harmonielehre, und dies mit dem Ziel, für eine gegebene Komposition zu jedem Akkord einen Riemannschen Funktionswert anzugeben, der den Verlauf der Harmonien des Stücks sinnvoll widerspiegelt.
Dabei stösst man auf nicht wenige Probleme:
- Riemann selbst hat das Programm, jedem möglichen Akkord einen Funktionswert zuzuschreiben, nie durchgeführt, nur für einige bekannte Akkorde (Dur-Dreiklänge etc.) ist dies geschehen.
- Es ist nicht klar unter Musikwissenschaftlern, was diese Funktionswerte eigentlich für eine Rolle spielen, und wovon sie exakt abhängen, siehe auch die Diskussion von Dahlhaus in loc.cit.
- Es ist nicht klar, was eine Tonart ist.
- Es ist nicht klar, wie ein Funktionswert von einer Tonart abhängen soll, und wie vieldeutig diese Wertmöglichkeiten sind.
- Es ist bei möglichen Vieldeutigkeiten nicht klar, welche Werte im Kontext eines Musikstückes zu bevorzugen sind, ja es ist nicht einmal klar, wann man in einer bestimmten Tonart ist...
- Es ist genau besehen nicht einmal klar, was ein Akkord sein soll in einer konkreten Komposition!
Wir wollen diese Probleme alle abarbeiten, bis wir die Implementierung der Theorie (d.h. des Torsos einer Theorie) erstellen können.
Problem 6 (Es ist genau besehen nicht einmal klar, was ein Akkord sein soll in einer konkreten Komposition.)
Dies lösen wir dadurch, dass die Software die Komposition zunächst auf eine Mengen von Noten mit E, H,D reduziert und dann gewissen Folge Ch_1,Ch_2,..., Ch_i, Ch_{i+1},...,Ch_N von Denotatoren des Typs
ChordEvent:.Limit(Onset,Chord);
Chord:.Powerset(H);
Onset:.Simple(R);
Wie sie das macht? Es werden zwei Methoden: Erstens einfach die Mengen von Noten gleicher Einsatzzeit gruppieren, zweitens Gruppen erzeugen jedesmal, wenn man Notengruppen hat, die grad anfangen zu dauern, oder wo das Ende der Dauer einiger Noten stattfindet, während noch andere weiterdauern. Das ist zwar relativ grob, aber es zeigt eine erste Auswahl an Varianten, um die Akkordsequenz zu erzeugen. Dies führt zur Akkordliste, die man im Hauptfenster erstellt:

Bild 101h1: Main window der HarmoRUBETTE
Problem 4 (Es ist nicht klar, wie ein Funktionswert von einer Tonart abhängen soll und wie vieldeutig diese Wertmöglichkeiten sind.)
Wir benutzen die drei Grundwerte der Riemann-Theorie: Tonikal (T), Dominantisch (D) und subdominantisch (S). In C-Dur hat
der Dreiklang c,e,g den Wert T, der Dreiklang g,h,d den Wert D und der Dreiklang f,a,c den Wert S. Wir nehmen davon je zwei Varianten: Dur und Moll, in Kleinbuchstaben für Moll, d.h., T,D,S, t,d,s. Die Semantik lassen wir momentan noch offen. Ferner wollen wir erlauben, dass in jeder Tonart einer der sechs Werte eingenommen werden kann. Wir lassen entsprechend den zwölf chromatischen Gruntönen (mod. Oktave) 12 Tonartsymbole zu C, Cis (=Des), D, Dis, E, F, Fis, G, Gis, A, Ais, H. Das ergibt also 72 mögliche Werte (Funktionswert,Tonart).
Wir erlauben uns aber noch mehr: Da es nicht klar ist von der Musiktheorie her, ob ein Akkord eigentlich mehrere Werte haben kann, und ob er das nur digital entweder hat oder nicht, oder ob verschiedene Werte mehr oder weniger angenommen werden können, haben wir uns für einen fuzzy Ansatz entschlossen: Ein Akkord Ch kann einen der 72 Werte annehmen als nicht-negative reelle Zahl. D.h. wir bekommen 72 Werte F(Ch,Funktionswert,Tonart) in R für den Akkord Ch. Wir erhalten dann entsprechend einer noch zu beschreibenden Methodepro Akkord eine 6 x 12 Matrix mit den 72 Werten von Ch. Diese Werte sind nur ein Potenzial und hängen noch nicht vom Kontext des Musikstücks ab. Bild 101h2 zeigt diese Matrix, die wir Riemann-Matrix nennen, für einen Akkord. Dunkle Rechtecke bedeuten hohe Werte, helle Rechtecke bedeuten niedrige Werte.
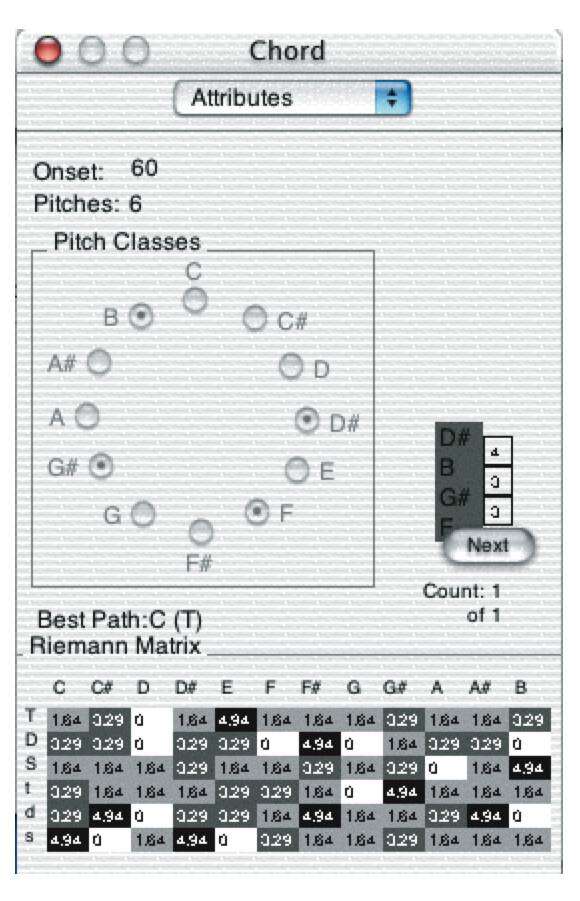
Bild 101h2: ChordInspector window der HarmoRUBETTE
Problem 1,2,3
Nun müssen wir implementieren, wie die Werte der Riemann-Matrix zu berechnen ist. Dazu offeriert die HarmoRUBETTE verschiedene Methoden, auch von verschiedenen Autoren verantwortet. Die Methode ist im Hauptfenster unter "Calculation Method" via Pop-Up-Button spezifizierbar. Wir können hier nicht auf die Einzelheiten eingehen. Bild 101h3 zeigt ein Fenster mit Riemann-Preferences nach der Mazzola-Methode, welche die Werteberechnung bedingen, und zwar im oberen Bereich "Function Scale Matrix". Die Idee bei dieser Methode ist es, jedem Ton eine Bewertung für die 72 Werte zuzuordnen und dann Terzketten zu betrachten, davon die Werte zu berechnen und schliesslich Akkorde hinsichtlich der minimalen Terzketten zu bewerten, die sie enthalten. Details finden sich im entsprechenden Abschnitt 41.3 HarmoRUBETTE von "The Topos of Music".
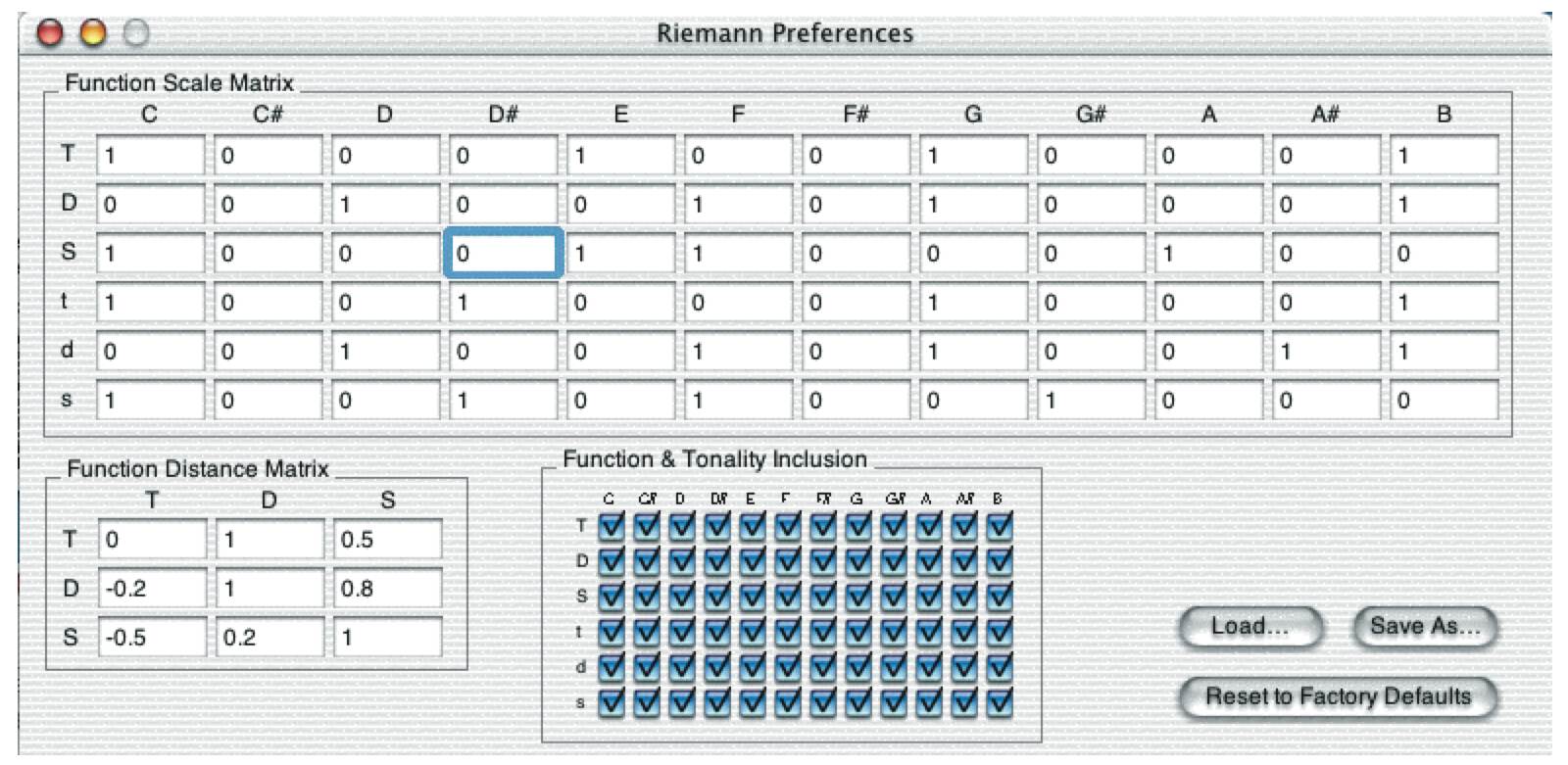
Bild 101h3: Riemann preference window der HarmoRUBETTE
Problem 5 (Es ist bei möglichen Vieldeutigketen nicht klar, welche Werte im Kontext eines Musikstückes zu bevorzugen sind, ja es ist nicht einmal klar, wann man in einer bestimmten Tonart ist.)
Bisher haben wir für jeden Akkord Ch_i unserer Folge Ch_1,Ch_2,..., Ch_i, Ch_{i+1},...,Ch_N eine Riemann-Matrix errechnet. Diese gibt das Potenzial der möglichen Werte an, aber nicht einen sinnvollen Wert. Der letzte Schritt unserer Berechnung wird nun jedem Akkord Ch_i eine Position F(Ch_i) =(Fun_i,Ton_i) zuordnen in der 6 x 12 Matrix, und damit natürlich auch den Wert an jener Stelle. Damit bekommen wir also einen Pfad
F(Ch_1),F(Ch_2),...,F(Ch_i),F(Ch_{i+1},...F(Ch_N)
durch die Riemann-Matrizen, welcher also die harmonische Semantik hier als Syntagma darstellt. Man muss aber dabei bedenken, dass die Vielfalt der a priori möglichen Wege bei beispielsweise 200 Akkorden (sehr wenig!!!) 72^200 = 2.9275160*10^371, also mehr ergibt, also man sich je wird mit einer Maschine berechnen können.
Bevor wir dieses kombinatorische Problem angehen, wollen wir aber die Wege bewerten: Welches sind gute, sinvolle Wege, welche sind harmonisch schlecht? Die Idee ist, dass wir die Übergänge zwischen zwei Positionen in der Riemann-Matrix bewerten wollen. So soll es billig sein, die Tonart zu behalten, aber teuer, sie zu wechseln. Es soll auch billig sein, von der Dominante in einer Tonart zur Tonika zu gehen, während es teuer ist, den umgekehrten Weg zu gehen, etc. Und dies auch in Abhängigkeit von den gegebenen Werten in der Riemann-Matrix. Solche Übergangsgewichte sind in der Riemann preference window in Bild 101h3 unten links angegeben, während dort sogar unten in der Mitte gewisse Positionen der Matrix ganz verboten werden können (weil man etwa "weiss", dass das Stück in einer festen Tonart sein muss). Auch die Präferenzen bezüglich Übergänge von Dominante zu Tonika etc. sind bewertbar, siehe dazu Bild 101h4:

Bild 101h4: Tonality preference window der HarmoRUBETTE
Auf Grund dieser Übergangspräferenzen wird nun grundsätzlich der besten harmonische Weg berechnet. Allerdings müssen wir dabei noch die Kombinatorik in den Griff bekommen, die ja wie oben gezeigt, so nicht beherrschbar ist.
Die Idee ist, dass wir nicht die langen Wege der ganzen Komposition anschauen können, sondern hier eine Auwahl treffen sollten. Wir haben dazu die Frage zu lösen, welcher harmonische Wert (Position in der Riemann-Matrix) für einen Akkord Ch_i zu wählen sei. Es ist plausibel, dass dieser Wert nicht von allen möglichen Akkorden der ganzen Komposition abhängen sollte. Das bedeutet, wir betrachten um einen Akkord herum nur Wege einer gewissen Länge vom Index i-k bis zum Index i+l. Für eine solche Wahl von "kausaler Tiefe k" und "finaler Tiefe l" berechnet man den besten "lokalen Weg" und kriegt daraus die Position für diesen Akkord Ch_i. Es zeigt sich, dass schon Werte von k = l = 3 grosse Rechenzeiten erfordern.
Hier ist ein interessantes Forschungsthema aus dem Bereich Berechnungskomplexität und auch Implementierung schneller Algorithmen oder statistischer Verfahren eröffnet. Das Resultat ist als harmonischer Pfad in Bild 101h5 gezeigt:

Bild 101h5: Riemann path window der HarmoRUBETTE
Wenn diese Riemann-Werte gerechnet sind für den Pfad, dann werden die Gewichte der Akkorde aus den Gewichten in der Riemann-Matrix und aus den Übergangsgewichten der Präferenzen gerechnet. Um schliesslich die Gewichte der Töne in Akkorden zu bekommen, werden die Rollen der Töne zur Bildung der Riemann-Gewichte betrachtet, d.h., man rechnet die Riemann-Matrizen mit einem Ton und ohne ihn und betrachtet dann den Quotienten der beiden Zahlen, um diese mit dem Akkordgewicht zu multiplizieren.
Die PerformanceRUBETTE
Wir wollen eine zentrale Anwendung der analytischen Gewichte aus den entsprechenden Rubetten diskutieren: die PerformanceRUBETTE. Damit können aus gegebenen Partituren (die wir als Denotatoren speichern und zur Verfügung haben) Aufführungsinterpretationen, d.h. Performances, gestalten.
Wir werden also nur einen ganz speziellen Aspekt der Performance-Forschung streifen: die Performance, welche durch Informationen analytischer oder "rationaler" Natur gestaltet werden. Neben diesen Begründungen und Motivationen, ein Stück zu performen, gibt es im wesentlichen noch dies (siehe Bild 102):
- die Motivation durch Emotionen, also eine psychologische Begründung. Vertreter dieser Richtung ist etwa der Musikpsychologe Alf Gabrielsson.
- die Motivation durch gestische Elemente, also eine physikalische Begründung. Vertreter dieser Richtung ist etwa Neil Todd.
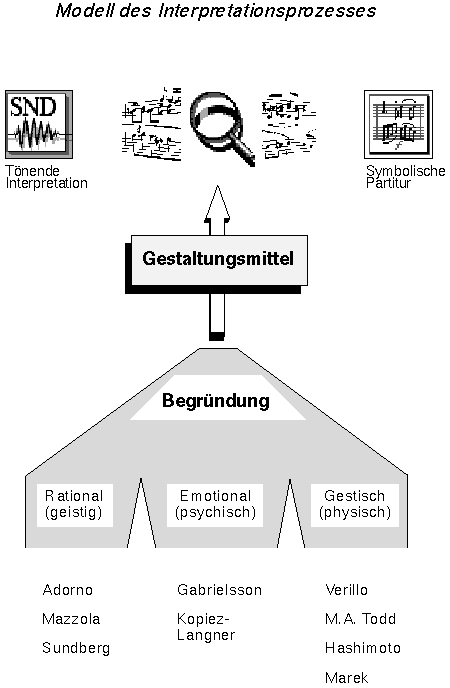
Bild 102: Models of Performance
Bevor man aber eine Performance gestalten kann, muss man ihre Struktur beschreiben.
Es handelt sich jedenfalls darum, einen Denotator bestehend aus Noten und ähnlichem Material auf der mentalen Ebene in einen Denotator bestehend aus Events auf der physikalischen Ebene zu transformieren.
Um die Ideen hier klarer zu machen, wollen wir der Einfachheit halber annehmen, dass wir es nur mit einer lokalen Komposition für Klavier, also einem Denotator
NoteSet:@Loc-Notes({N1,N2,...,Ns})
von Klaviernoten Ni, d.h. Note-Denotatoren, zu tun haben, wobei wir in diesem Kontext die Form
Note:.Product(Einsatzezeit,Tonhöhe,Lautstärke,Dauer);
Einsatzzeit:.Simple(R);
Tonhöhe:.Simple(R);
Lautstärke:.Simple(R);
Dauer:.Simple(R);
und die Form
Loc-Notes:.Powerset(Note);
annehmen. Ein solcher Noten-Denotator Ni habe dann die Koordinaten-Werte (Koordinaten-Namen spielen momentan keine Rolle) E, H, L, D, d.h.
Ni:@Note(E,H,L,D)
Auf der physikalischen Seite haben wir auch eine lokale Komposition der entsprechenden Events EventSet ={n1,...,ns}, ein Denotator
EventSet:@Loc-Events({n1,n2,...,ns})
der Form
Loc-Events:.Powerset(Event);
mit
Event:.Product(einsatz,höhe,laut,dauer);
einsatz:.Simple(R);
höhe:.Simple(R);
laut:.Simple(R);
dauer:.Simple(R);
als physikalisch Koordinaten in Sekunden etc. Wir schreiben ein Event ni entsprechend mit Kleinbuchstaben als ni:@Event(e,h,l,d).
Mit diesen Notationen kann man also die Performance-Transformation als eine Funktion P anschauen
siehe auch Bild 103.
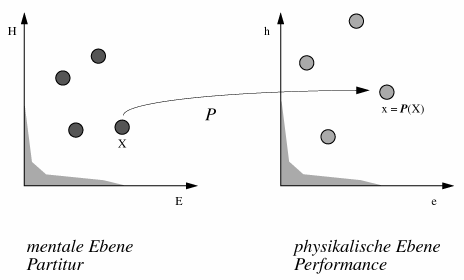
Bild 103: Die Performance-Transformation P
Die Struktur solcher Transformationen wollen wir hier nicht näher diskutieren, dazu wäre zu viel Mathematik notwendig.

Bild 104: Escher: Balcony, eine Metapher für die Verformung einer LPS
Wir wollen uns aber fragen, wo man eingreifen soll, um P zu gestalten.
Dabei müssen wir zunächst beachten, dass man ja nie eine Peformance gleich in einem Schritt endgültig gestaltet! Man übt, und dies ist ein mehrstufiger Verfeinerungsprozess, der in wirklichkeit Jahre dauern kann. Dies führt zum Begriff des Stemmas (siehe Bild 105). Das bedeutet, dass man zunächst mit eine "Prima-Vista-Performance" anfängt, also dem erste Einspielen des Stücks, ohne Raffinesse, sondern gemäss den geschriebenen Anweisungen ganz "wörtlich" wiedergegeben.
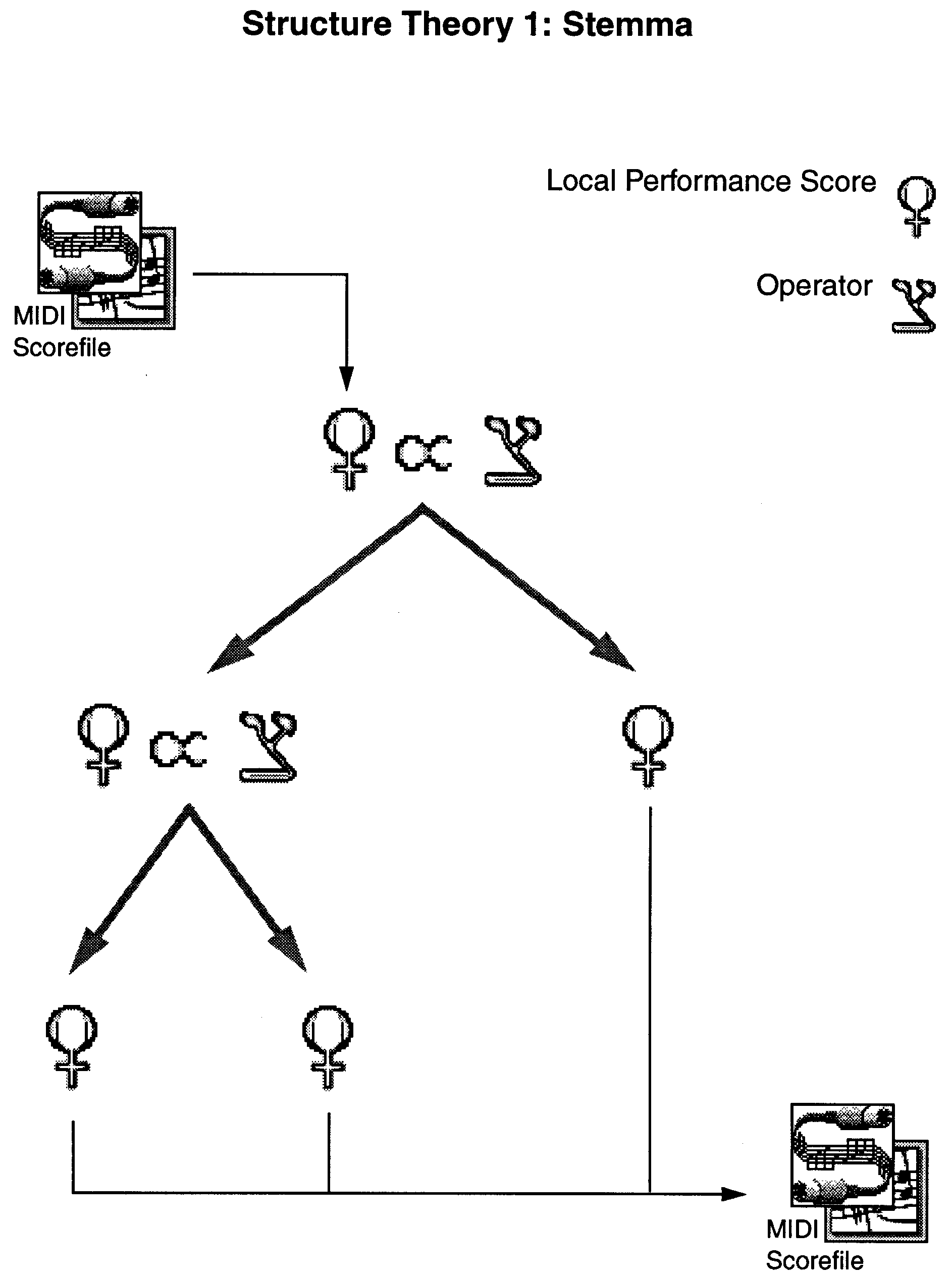
Bild 105: Stemma
Nach und nach wird die Spielweise verfeinert, und das geschieht genealogisch: Man benutzt das schon Gelernte und baut das aus, setzt raffiniertere Varianten hinzu. Dies geschieht oft auch durch Aufteilung des Materials in kleinere Ausschnitte. Ein solcher sukzessive entstehender Ausschnitt (etwa eine Periode, ein Takt, eine Stimme) heisst in der Performance-Theorie
Local Performance Score (=LPS). Eine LPS ist so etwas wie eine lokale Einheit der Performance-Gestaltung. Bild 106 zeigt eine LPS mit ihren Bestandteilen so, wie sie es in RUBATO implementiert ist.

Bild 106: Die Struktur einer LPS
Wir erkennen diese 10 Bestandteile:
- Mother: die LPS, von der unsere LPS durch Verfeinerung abgeleitet wurde
- Daughters: Die diversen LPS, die von unserer LPS später abgeleitet wurden
- Operator: Das Gestaltungs-Werkzeug, welches für die Verfeinerung unserer LPS verantwortlich ist
- Weights: die analytischen Gewichte, die der Operator für seine Gestaltung benutzt hat
- Instrument: das Instrument, welches für die Performance benutzt wird
- Initial Set: eine Menge der Noten, auf die sich die Performance als "Startmenge" bezieht; z.B. der Kammerton a' oder eine erste Einsatzzeit, von der aus man weiterzählt
- Initial Performance: die Performance, welche auf dem Initial Set schon definiert ist, also z.B. die 440 Hz, welche dem Kammerton zugeordnet sind, oder die physikalische Startzeit zur ersten Einsatzzeit in der Initial Set
- Symbolic Kernel: die lokale Komposition der "Noten" (in der obigen Notation NoteSet), die gespielt werden soll
- Performance Kernel: die lokale Komposition der "Events" (unser obiges EventSet), die als gespielte Noten auftreten, also das P-Bild des Symbolic Kernels
- Hiararchy and Space Frames: eine Reihe von technischen Rahmenbedingungen worüber man die Performance grundsätzlich erstrecken wird.
Man kann nun die Verfeinerung oder "Verformung" (siehe Bild 107) der von der Mother übernommenen Performance-Transformation P durch den Operator auf drei Arten gestalten:
- direkte Beeinflussung der Events der Mother, also Eingreifen in das Performance-Resultat der Mutter;
- direkte Beeinflussung der Notes der Mother, also brutale Veränderung der Noten der Mutter
- Veränderung der Verformungsgrade von P, etwa via Einflussnahme auf das Tempo-Kurve der Mutter LPS.
- Aufspaltung der LPS in mehrere kleinere LPS
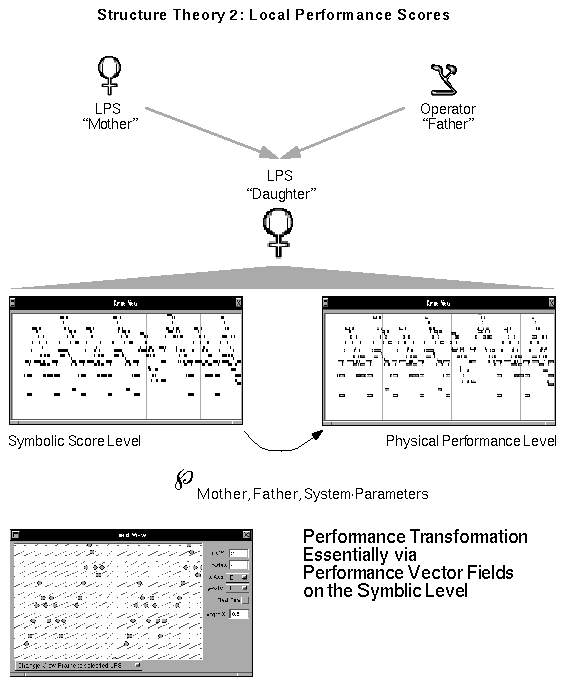
Bild 107: Performance-Transformation auf einer LPS
In RUBATO sind diese Möglichkeiten durch entsprechende Operatoren realisiert worden. Wir wollen hier nur zwei Operatoren anschauen: den PhysicalOperator für die erstgenannte Aufgabe, und den TempoOperator für die an dritter Stellen genannte Aufgabe.
PhysicalOperator
Angenommen, man hat ein metrisches Gewicht MetroWeight errechnet, dann hat man zu jeder Einsatzzeit E ein Gewicht MetroWeight(E) und kann dies auf irgendeinen oder mehrere Parameter der Events anwenden. Die Wirkung ist wie folgt (siehe Bild 108).
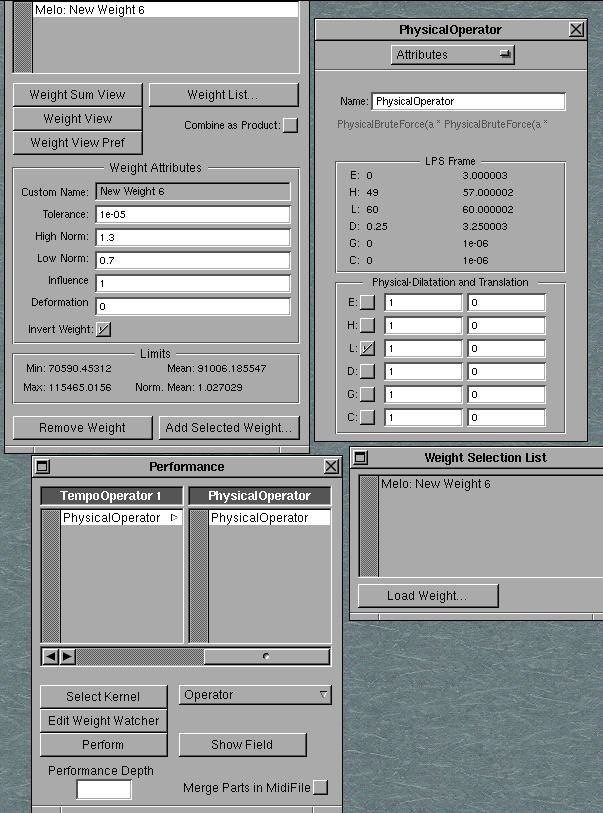
Bild 108: Inspector des PhysicalOparator
Man aktiviert erstens bestimmte physikalische Parameter durch Anwählen des Häkchens. Man wählt dann für jeden durch ein Häkchen aktivierten physikalischen Parameter s des Events x = P(X) eine Transformation a.s+b, und dann wird dieser neue Wert jeweils mit dem Gewicht MetroWeight(X) der Note X zum physikalischen Event x multipliziert, wie im WeightWatcher eingegeben wird (siehe Bild 109).
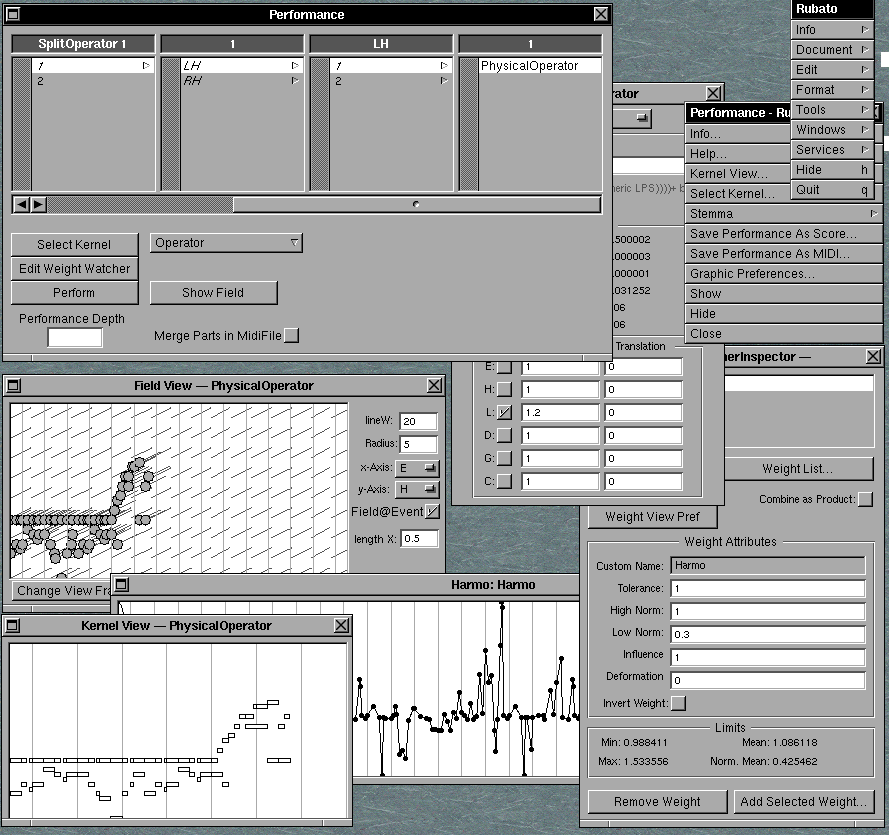
Bild 109: WeightWatcher-Window
Im WeightWatcher kann man die Grenzen für Maximal- und Minimalwerte eines Gewichts einstellen, z.B. von 0.8 bis 1.2. Dann wird unser Gewicht G(E) in diesen Grenzen verzerrt, ergibt G*(E), und wir haben für jeden aktivierten Parameter s des Events x den Wert G(E)*(a.s+b).
Die Wirkung des metrischen Gewichts MetroWeight auf die Lautstärke L hatten wir bei der linken Hand in der Träumerei schon gehört.
Als interessante Anwendung kann man auch das metrische Gewicht direkt auf die Tonhöhen wirken lassen und so eine Sonifikation der Analyse erzeugen, also ein Hörbarmachen einer Analyse, wodurch man sehr schnell Strukturen vernimmt, die man nicht sehen würde. Wir hören uns dies im Fall der Kunst der Fuge an.
Audio 11: Sonifizierung der metrischen Analyse in der Kunst der Fuge (Joachim Stange-Elbe)
TempoOperator
Dieser Operator wirkt weder auf mentale noch auf physikalische Parameter, sondern ändert die Beziehung zwischen ihnen. Typisch für diese Beziehung ist das Tempo. Es ist definiert als
(eigentlich dE/de, aber als Funktion von E). Das ist ja die mathematisch sauber übersetzte Bedeutung von "M.M. = ...Viertelnoten/Minute" (M.M. = Maeltzel Metronom) an einer bestimmten Stelle der Partitur!
Das Tempo sagt also, wie sich die physikalische Einsatzzeit ändert in Relation zur mentalen Einsatzzeit. Der TempoOperator macht nun folgendes: Wir gehen aus von einem Tempo T(E), das von der Mutter der LPS übernommen wird. Am Anfang wird das meist ein konstantes Tempo sein, möglicherweise mit ein paar festgeschriebenen Ritardandi oder Fermaten. Nun aber haben wir ein Gewicht und seine Verzerrung G* auf dem WeightWatcher. Damit wirken wir auf das Mutter-Tempo, indem wir statt T(E) nun
nehmen. Das zweite Fenster von oben in Bild 110 zeigt die Wirkung eines melodischen Gewichtes auf die physikalischen Einsatzzeiten.
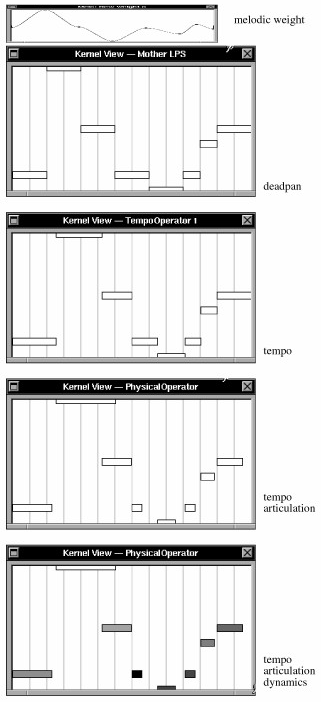
Bild 110: Tempo-Veränderung mit dem MeloWeight beim 8-tönigen Hauptthema der Kunst der Fuge
Bevor wir hier weiter gehen, wollen wir kurz eine Tempo-Hierarchie, also ein Stemma im Bereich des Tempo anschauen, wie sie schon anfangs der 90er Jahre durch die software presto, die wir in
Kapitel 10 anschauen werden, implementiert wurde.
Tempo-Hierarchien
Wir hatten bei unseren Untersuchungen der Literatur zur Agogik (=Feinstruktur des Tempo) beobachtet, dass klassische Anweisungen, wie etwa die von Carl Czerny, nichts bringen.
Als eines der repräsentativen Traktate zur Vortragskunst des Tempos, diskutiert Danuser im NHB, Bd.11 Carl Czernys Vollständige theoretisch-praktische Pianoforte-Schule op. 500 um 1840. Beispiel: Bild 111..

Bild 111: Czerny, §7
Der Informatiker und Musikwissenschaftler
Oliver Zahorka, mein Mitarbeiter am RUBATO-Projekt 1992-1996, hat die Anweisungen von Czerny mit dem AgoLogic-Modul der Software
presto untersucht und so genau wie möglich zu simulieren versucht (Bild 112).
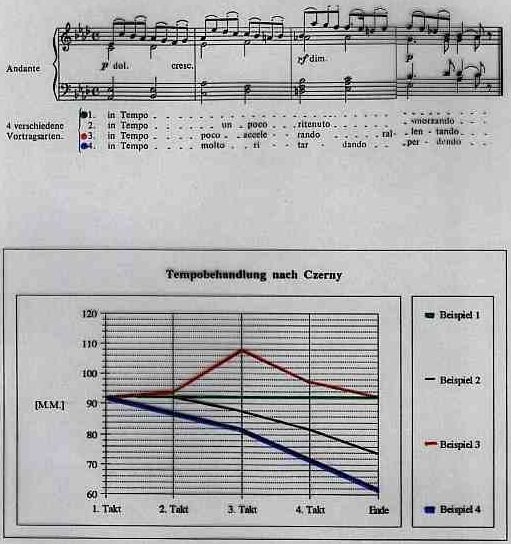
Bild 112: Czerny nach Zahorka
Audio 12: Tonband Czerny: Versionen 1, 3 und 4
Dies klingt unbefriedigend. Wir vergleichen dies mit einer Interpretation auf der
presto-Software nach Zahorka, mit gebundenem Rubato.
Audio 13: Tonband Czerny: Version Zahorka
Dies wird mit der AgoLogic-Funktion in
presto hergestellt (Bild 113).

Bild 113: presto-Bild der Hierarchie
Dies sieht bei der Czerny-Situation oben so aus, siehe Bild 114. Die linke Hand wirkt als Referenz-Agogik und lässt die rechte Hand frei variieren, solange sie am Ende jedes Taktes wieder mit der Linken zusammenkommt.
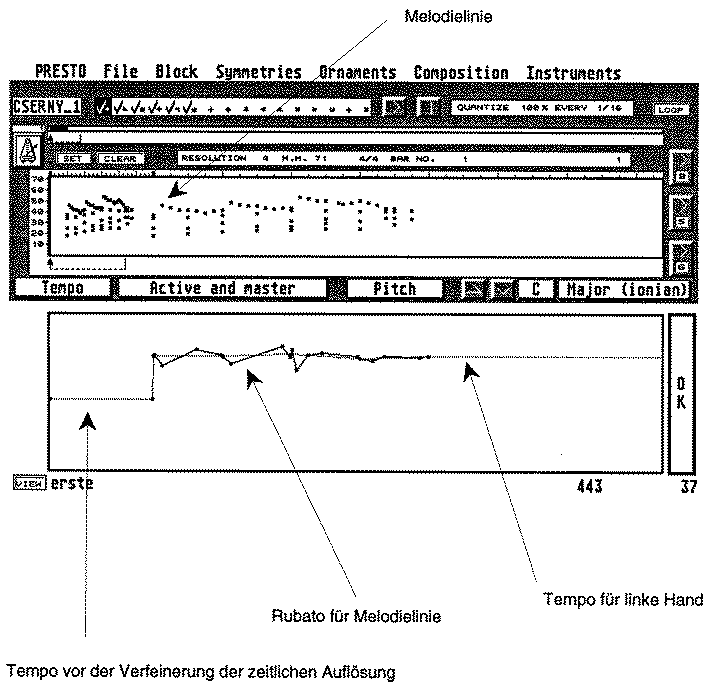
Bild 114: presto-Bild der Czerny-Hierarchie nach Zahorka
Folgt ein Beispiel in diesem Geist:
Chopin,
Impromptu op. 29 (Bild 115).

Bild 115: Chopin-Partitur: Impromptu op. 29; Ausschnitt mit Triller und Arpeggi
Die entsprechende Tempo-Hierarchie ist in Bild 116 dargestellt. Die halben Noten in diesem Ausschnitt die Mutteragogik. Sie haben als Töchter die Arpeggio-Tochter und die Triller-Tochter. Die Arpeggio-Tochter hat dazu noch eine Arpeggio-Enkelin.
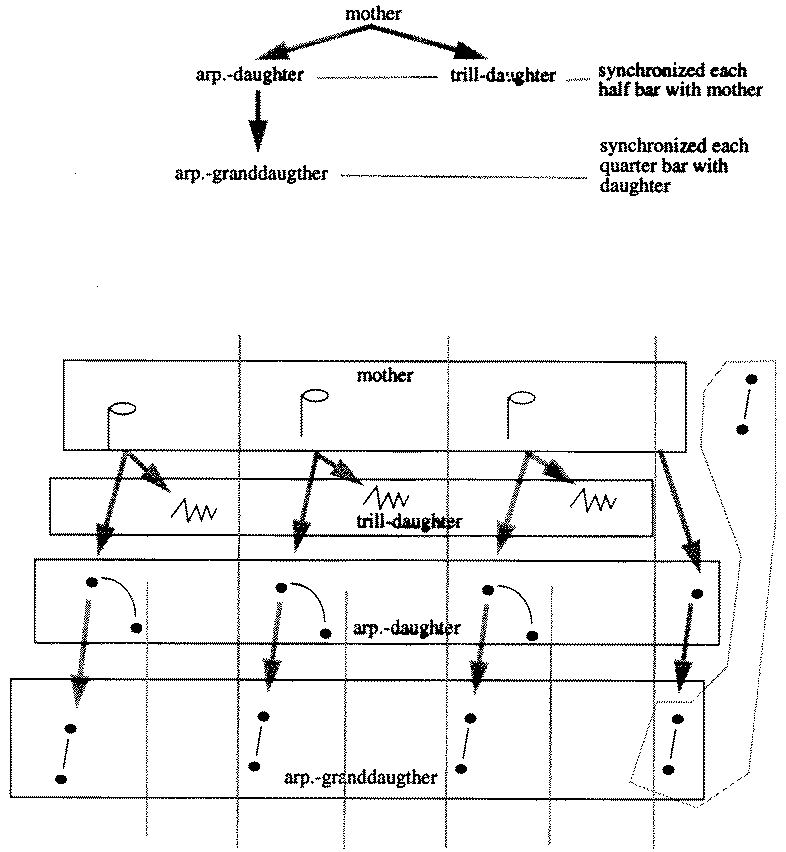
Bild 116: Chopin-Hierarchie
Audio 14: Diverse Versionen Chopin: Flach (= Deadpan), Anfänger, Alter Barenboim, Pollini
Ende Tempo-Hierarchien
Wir hören uns ein Beispiel der Gestalung des Hauptthemas der Kunst der Fuge an, wo ein melodisches Gewicht auf Agogik, Artikulation und Dynamik angewendet wird (siehe Bild 110 für die einzelnen Phasen).
Audio 15: Hauptthema Kunst der Fuge und dessen Gestaltung mit der PerformanceRUBETTE
Wir hören uns nun noch eine kurze Sequenz an einer Interpretation der kuriosen Geschichte, die wir 1996 mit dem Bösendorfer-MIDI-Flügel an der Staatlichen Hochschule für Musik in Karlsruhe als ersten Test hergestellt hatten (Bild 117 zeigt das Stemma):
Audio 16: Deadpan (Prima Vista, keine Gestaltung!)
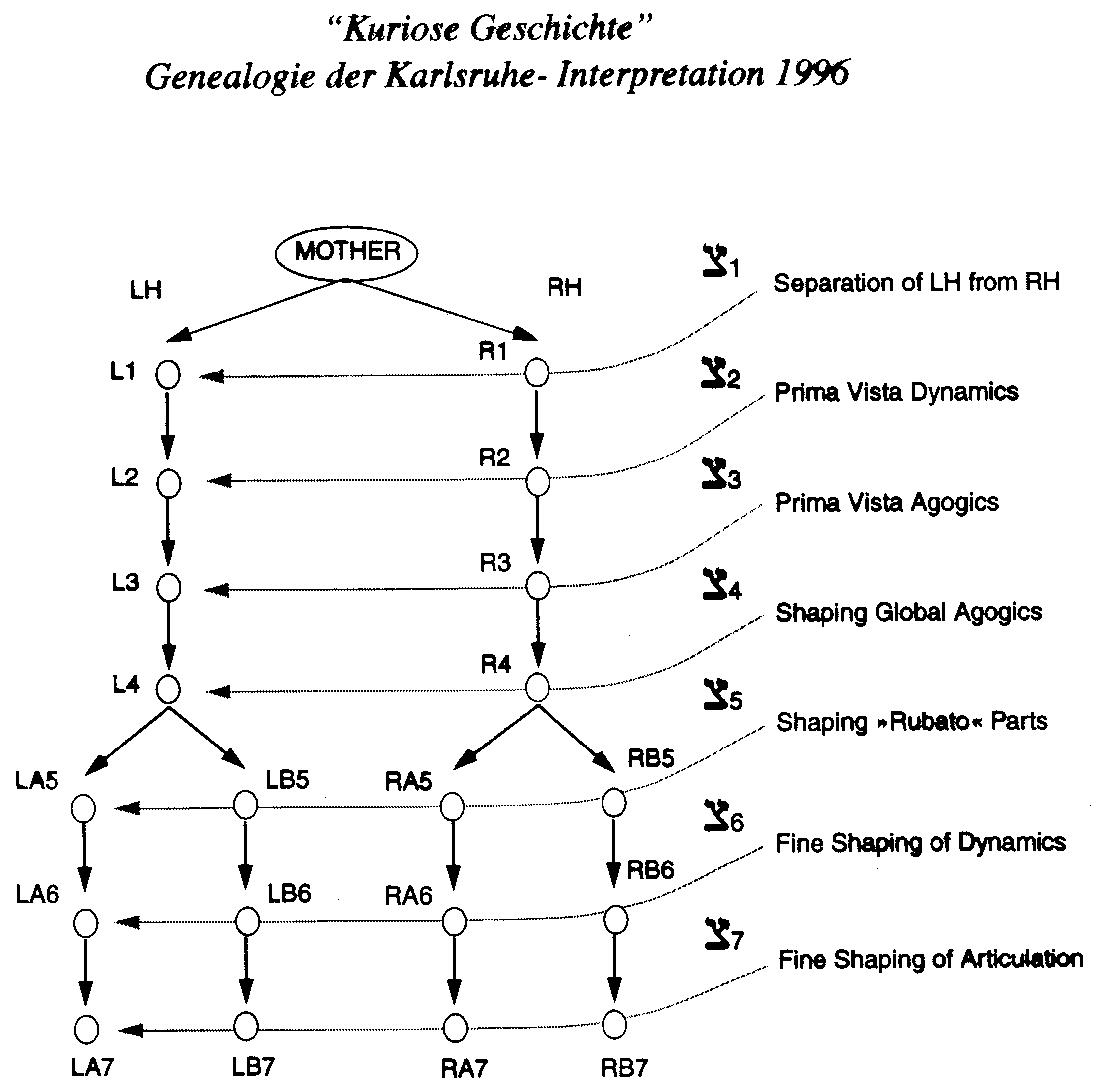
Bild 117: Stemma der RUBATO-Gestaltung
Audio 17: Gestaltung mit RUBATO
Audio 18: Vergleich mit Interpretation Martha Argerich
Audio 19: Vergleich mit Interpretation Tatjana Nikolajewa (1992)
Und zum Schluss wollen wir die Grenzen der Interpretation am Sopran der unvergleichlichen Florence Foster-Jenkins erkunden: das Wunder der menschlichen Stimme:
Audio 20: Florence Foster-Jenkins: Die Königin der Nacht aus Mozarts Zauberflöte
Wir diskutieren die Problematik der Interpretation und die Aufgabe einer Performance-Forschung.
 ZURÜCK ZURÜCK |
|
WEITER |
























