Wir erinnern daran, dass das physikalische Klangobjekt nur eine Schwingung ist, in der Regel von kurzer Ausdehnung und alles andere als regelmässig.

Bild 47: Konstruktion und Zerlegung von Soundobjekten
Die Konstruktion resp. Zerlegung wird nach verschiedensten Verfahren vorgenommen, von denen keines Exklusivität beanspruchen darf, auch wenn gewisse Verfahren historisch, technologisch, physiologisch oder psychologisch bestimmte Vorzüge oder Bedeutungen haben, siehe auch Bild 47. Dieses zeigt die mentale Konstruktion und Zerlegung resp. die physiologisch/technologische Synthese und Analyse von Sound-Objekten im Rahmen der allgemeinen Musik-Topographie.
Das Bild, das man sich von diesen "Perspektiven" eines Sound-Objekts machen muss, ist das der Darstellung eines Objekts als Punkt in einem Koordinatenraum. Wie in der Geographie ist die Darstellung (Kartesische Koordinaten, Polarkoordinaten, etc.) nicht mit dem Objekt zu verwechseln. Ferner ist es ein wesentlicher Unterschied, ob man ein mentales Verfahren angibt (z.B. die Fourier-Zerlegung via Partialschwingungen) oder ob man dieses Verfahren auch physiologisch/technologisch umsetzen kann.
Und oft sind die Annahmen, die eine bestimmte Darstellung erlauben, nicht selbstverständlich; wir werden das gleich sehen. Also:
| Immer, wenn Sie Darstellungen von Klangobjekten antreffen, zuerst die Bedingungen untersuchen, unter denen sie verkauft oder gekauft werden sollen! |
Die Fourier-Darstellung
Dies ist die klassische Darstellung, welche im 18. Jahrhundert als "Oberton-Zerlegung" bekannt geworden und anfangs 19. Jh. mathematisch bewiesen worden ist (der Mathematiker und Musiktheoretiker Pater Mersenne entdeckte die Obertöne anfangs des 17. Jh.; anfangs des 19. Jh. bewies der Mathematiker Joseph Fourier im Rahmen von Untersuchungen der Wärmeleitung die Partialtonzerlegung).
Die Fourier-Darstellung betrifft strikt periodische Funktionen f(t) der Zeit t, in unserem Fall periodische Auslenkungen des normalen Luftdrucks. Die Periodizität f(t+T) = f(t) mit Periode T und zugehöriger Frequenz F = 1/T wird mit Tonhöhenwahrnehmung assoziiert. Daher also der unmittelbare Zusammenhang mit der Musik.
Die Idee der Fourier-Darstellung von periodischen Funktionen basiert darauf, dass man eine bestimmte Sorte von solchen Funktionen quasi als Koordinaten-Achsen der Koordinatendarstellung einer periodischen Funktion nimmt und diese Funktion dann in diesem "Koordinatensystem" positioniert. (Diese Sprechweise ist im übrigen mathematisch vollkommen korrekt, also nicht nur eine Metapher.)
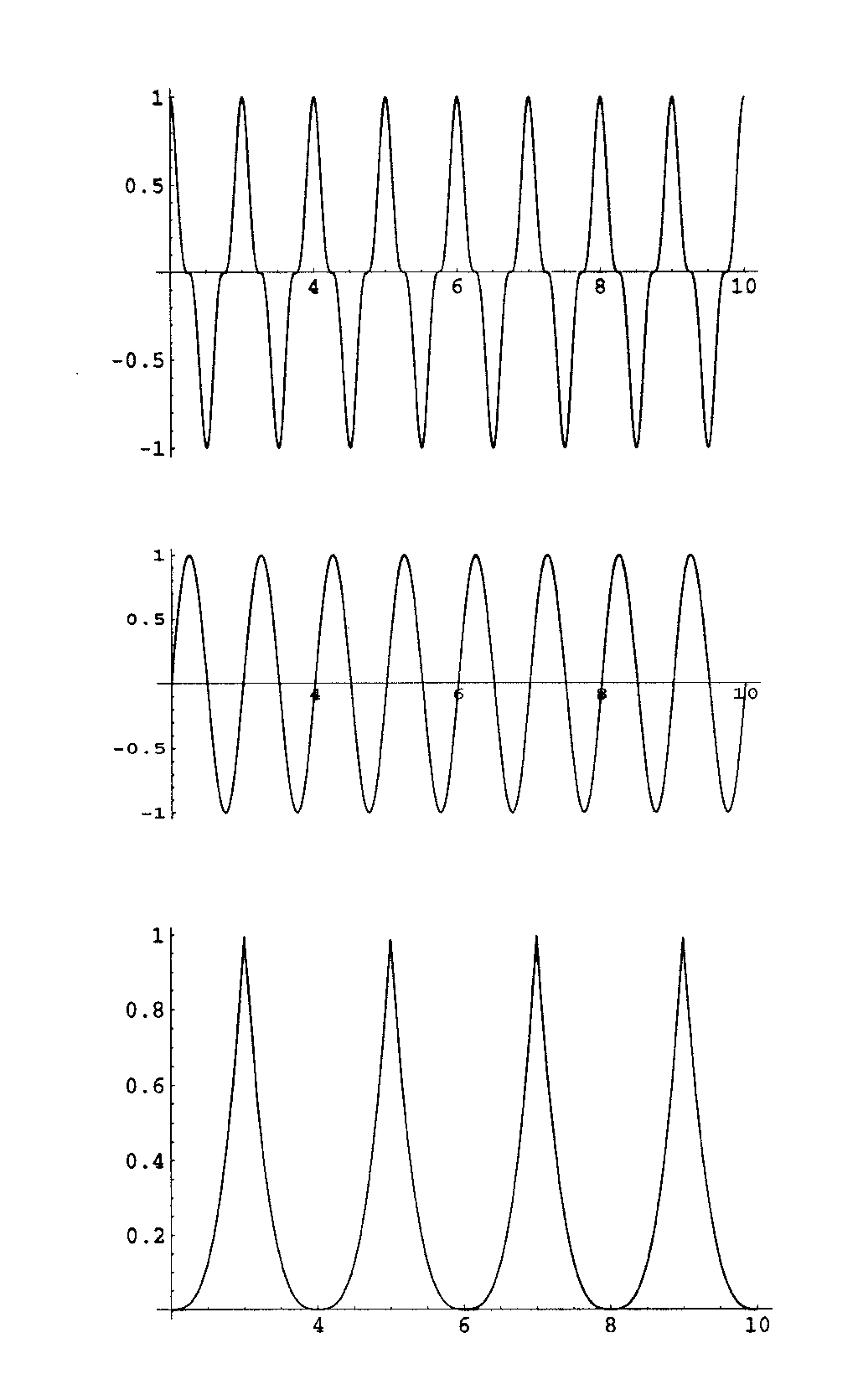
Bild 48: Periodische Funktionen h, g, f
Die Fourier-Darstellung geht aus von ganz speziellen solchen Funktionen, siehe Bild 48. Im Bild sieht man drei periodische Funktionen, deren mittlere zum durch Fourier ausgezeichneten Typus gehört. Diese Sorte Funktionen sind die Sinus-Funktion sin(t) und deren affine Verzerrungen, d.h. den Funktionen der Gestalt A.sin(B.t+C), A, B, C Konstanten. Darunter erkennen Sie den Cosinus: cos(t) = sin(Pi/2-t) (A=1,B=-1, C=Pi/2).
Diese Art von Funktionen sind wichtig in der Theorie der schwingenden physikalischen Systeme (zB. elastische Federn mit Massen, die daran hängen und durch eine äussere Kraft in Schwingung versetzt werden), da sie der Differentialgleichung sin''=-sin genügen, was für mechanische Schwingungssysteme ein Lösungsansatz der Newtonschen Differentialgleichungen kx = mx'' ist.
Mathematisch gesehen sind sie aber sehr kompliziert, so erfüllen sie etwa den tiefliegenden Zusammenhang mit der Exponentialfunktion: cos(x)+i.sin(x)=e^(i.x) . Es kann also nicht die Rede davon sein, dass Sinusfunktionen "elementar" seien. Wenn also in der musikalischen Akustik und ihrer "Metaphysik" von "reinen" Sinusschwingungen die Rede ist, muss das zumindest mathematisch zurückgewiesen werden: Sinusschwingungen gehören zum Kompliziertesten, was es gibt.
Nun kann man mit einem Arsenal von Funktionen verschiedene neue Funktionen produzieren, siehe Bild 49. Wir nehmen dazu die drei periodischen Funktionen h(t), g(t), f(t) (von oben nach unten) aus Bild 48. Die oberste Funktion in Bild 49 ist die Summe g(t)+ f(t), die mittlere Funktion ist eine Streckung ?.g(t), die unterste Funktion ist eine Streckung ?.f(t).
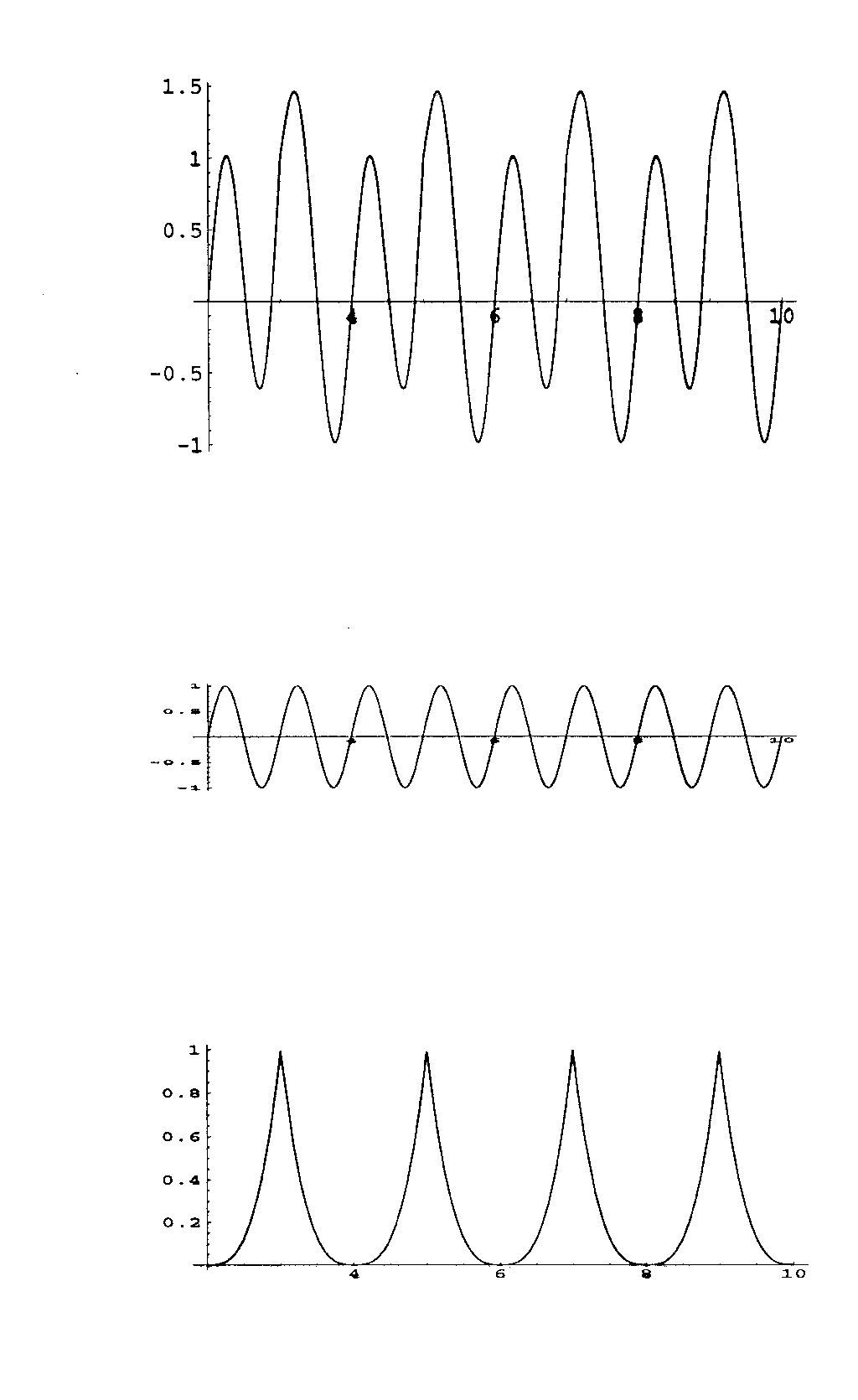
Bild 49: Summe und Streckung von Funktionen
Die Fourier-Darstellung benutzt diese sogenannte additive Methode der Erzeugung von Funktionen nach folgendem Satz:
| Sei f(t) eine periodische (stückweise differenzierbare) Funktion mit Periode -Pi,+Pi. Dann lässt sich f eindeutig so darstellen: f(t) = a_0 +Σ_{n=1,2,3,...} a_n.cos(nt)+b_n.sin(nt) |
Die a's und b's lassen sich aus f eindeutig berechnen, nämlich:
|
n=0: a_0 = (1/2Pi).Integral[-Pi,+Pi] f(t)dt 0<n: a_n = (1/Pi).Integral[-Pi,+Pi] f(t).cos(nt)dt 0<n: b_n = (1/Pi).Integral[-Pi,+Pi] f(t).sin(nt)dt |
Es gibt viele gleichwertige Darstellungen:
| Wenn die Funktion die Frequenz F hat, d.h. eine Periode von der Länge 1/F, dann lässt sich f so schreiben. f(t) = A_0 + Σ_{n=1,2,3,...} A_n.cos(2Pi.nF.t)+B_n.sin(2Pi.nF.t) |
(Achtung: die As und Bs berechnen sich dann nicht mit identischen Integralformeln wie oben! Aber der Unterschied ist nicht gross. Siehe das Kapitel Fourier Theory in Comprehensive Mathematics for Computer Scientists.)
Eine dritte Darstellung verwendet die Phasenverschiebungen der einzelnen n-ten Beiträge: Wenn wir für zwei Zahlen a,b, A = Wurzel(a^2 +b^2) setzen, dann gilt aus der Theorie der Sinusfunktion
a.cos(t)+b.sin(t) = A.sin(t+arccos(b/A)).
Daraus konstruiert man dann die dritte Darstellung:
| f(t) = A_0 + Σ_{n=1,2,3,...} A_n.sin(2Pi.nF.t+Ph_n) |
Man nennt die Beiträge A_n .sin(2Pi.nF.t+Ph_n) die n-ten Partialschwingungen, A_n die n-ten Amplituden und Ph_n die n-ten Phasenverschiebungen.
Ein Beispiel: die Sägezahnkurve mit Periode 2Pi: Sie hat Steigung 100% und beginnt alle 2Pi beim Wert -Pi und geht bis +Pi hinauf. Sie ist bis auf die periodisch wiederkehrenden Zacken stetig, erfüllt also die Bedingungen von Fouriers Satz. Bild 50 zeigt die Annäherung der Sägezahnschwingung durch die ersten drei Sinus-Beiträge. Man erkennt, dass sich schon nach wenigen Schritten der Aufsummierung der Partialschwingungen die Sägezahngestalt gut erkennen lässt.
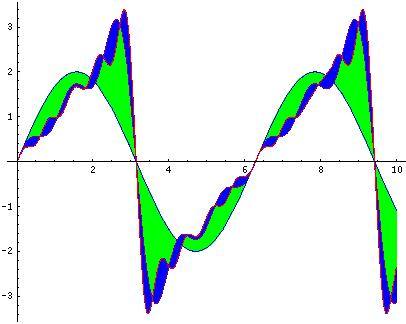
Bild 50: Die Sägezahnfunktion mit Periode 2Pi in der Annäherung durch die ersten drei Sinus-Beiträge
In der Praxis kann man natürlich nicht bis Unendlich aufsummieren. Man rechnet dann endliche Summen aus, die umso genauer werden, je höher man geht.
Es gibt noch ein Problem: In der Praxis sind natürlich keine periodischen Funktionen gegeben, sondern Schwingungen, die nur für eine endliche Dauer eine messbare Auslenkung aufzeigen. Um diese Schwingungen trotzdem via Fourier zu beschreiben, tut man so, wie wenn sie sich nach links und rechts unendlich oft wiederholen würden, man hängt also an das real existierende "Wellenpaket" Kopien desselben links und rechts beliebig oft dran und berechnet dann die Fourier-Darstellung dieser nun periodischen Funktion! Das ist zumindest grundsätzlich eine massive Veränderung der an sich gegebenen Schwingung!
Wir besprechen das in der Praxis wichtige Verfahren, aufgrund dessen die Fourier-Darstellung durch schnelle Algorithmen der FFT ( = Fast Fourier Transform) auf Computern auch rechnerisch beherrscht werden kann. Diese Technologie ist weit verbreitet und muss deshalb zumindest in den Grundzügen allen bekannt sein, damit man auch weiss (s. oben) was man tut, wenn man ein FFT-Programm auf eine Schwingung loslässt!
Man misst dabei die Luftdruckauslenkung f(t) in gleichen Zeitintervallen Δ insgesamt N = 2n Male (eine gerade Zahl zu nehmen ist eine rechnerisch begründete Konvention): zu den Zeitpunkten
-nΔ,..., -2Δ, -Δ, 0, Δ, 2Δ,..., (n-1)Δ,
siehe Bild 51.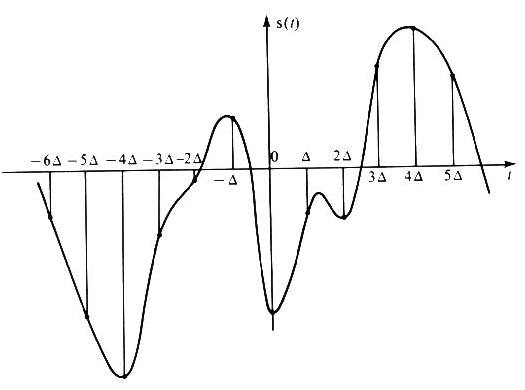
Bild 51: Messung einer Funktion an N = 2n Punkten für n = 6
Die Periode ist also definitionsgemäss
T = NΔ=2nΔ,
die Frequenz also
F = 1/T = 1/NΔ.
Dann rechnet man die Funktion an allen gemessenen Zeitpunkten mit einer Fourier-Summe aus wie folgt:
| f(rΔ) = a_0 + 2.Σ_{m=1,2,3,...,n-1} a_m.cos(2Pi.mF.rΔ)+b_m.sin(2Pi.mF.rΔ)+
a_n.cos(2Pi.nF.rΔ) |
Diese Gleichung soll gelten für alle N = 2n Messwerte. Hier ist die Zahl der Summanden willkürlich. Aber es hat Sinn: Wir erhalten so 2n lineare Gleichungen mit 2n Unbekannten a_0 , a_1 ,...,a_n ; b_1 , b_2 ,..., b_(n-1) .
Man kann zeigen, dass das obige Gleichungssystem immer genau eine Lösung besitzt.
Kurze Begründung für Mathematik-Interessierte:
Wir haben dann die folgende Matrix-Darstellung:
f(*Δ)^t = M.(a_0 , a_1 ,...,a_n ; b_1 , b_2 ,..., b_{n-1} )^t ,
wobei X^t transponierte Matrix, also Spaltenvektoren, bedeutet und M eine quadratische 2n-Matrix ist.
Die gemessene Zeitreihe f(*Δ) wird also geschrieben als Linearkombination der Zeitreihen
C_m = cos(2Pi.mF(-nΔ)),...cos(2Pi.mF(n-1)Δ) für alle m=0,...n,
S_m = sin(2Pi.mF(-nΔ)),...sin(2Pi.mF(n-1)Δ), m=1,...,n-1.
Geht das immer? Ja, denn man beweist in der Analysis, dass diese Vektoren C_m und S_m linear unabhängig sind, dh. die Determinante der Matrix M ist von Null verschieden, und wir können deren Inverse bilden.
Ende der kurzen mathematischen Einschiebung.
Wir werden im folgenden Kapitel im Detail auf die endliche Fourier-Zerlegung, auf den FFT-Algorithmus und auf die Datenkompression mp3 eingehen.
Die Darstellung benutzt also die Fourier-Darstellung bis zur n-ten Partialschwingung. Wir haben also die
Grundfrequenz F = 1/NΔ.
Ferner istdie höchste beteiligte Frequenz nF = n.1/NΔ=1/2Δ.
Das entspricht einer Periode von 2Δ, was heisst, dass man die Periode der höchsten Frequenz zweimal abtastet!
| Diese Frequenz 1/2Δ heisst Nyquist-Frequenz der endlichen Fourierzerlegung. |
Beispiel:
Die Musik-CD benutzt als Abtastfrequenz 44.1 kHz, was das Doppelte der höchsten Hörfrequenz von Sinustönen im menschlichen Ohr ist, wenn man ausgeht davon, dass die cochleare Schallzerlegung mit der Fourierzerlegung etwas zu tun hat, was nicht genau abgesichert ist (siehe etwa Pierre Buser, Michel Imbert: Audition).
Oft erreicht man in der Praxis bessere Resultate, wenn man nicht das gesamte Signal, sondern nur kurze Zeitfenster je für sich Fourier-analysiert. Bild 52 zeigt das Beispiel eines Trompetenklanges, der über 0.5 Sekunden dauert (Achse nach rechts). Man unterteilt diesen Zeitraum in viele kurze Abschnitte und führt für jeden dieser Abschnitte eine endliche Analyse durch nach dem obigen Muster. So wird auch der zeitliche Verlauf einer Schwingung durch veränderliche Fourierzerlegung dargestellt. Das in Bild 52 dargestellte, so genannte Chronospektrum zeigt für jeden Zeitpunkt die Amplituden der Partialschwingungen bis zur 13. Partialschwingung. Die Darstellung ist allerdings etwas unehrlich: Es sieht aus, wie wenn man in jedem Zeitpunkt eine Fourier-Darstellung hätte, wo man doch in Wirklichkeit nur eine dichte Folge von Zerlegungen besitzt. Diese diskreten Werte werden in der Graphik zu kontinuierlichen Kurven zusammengesetzt (interpoliert).
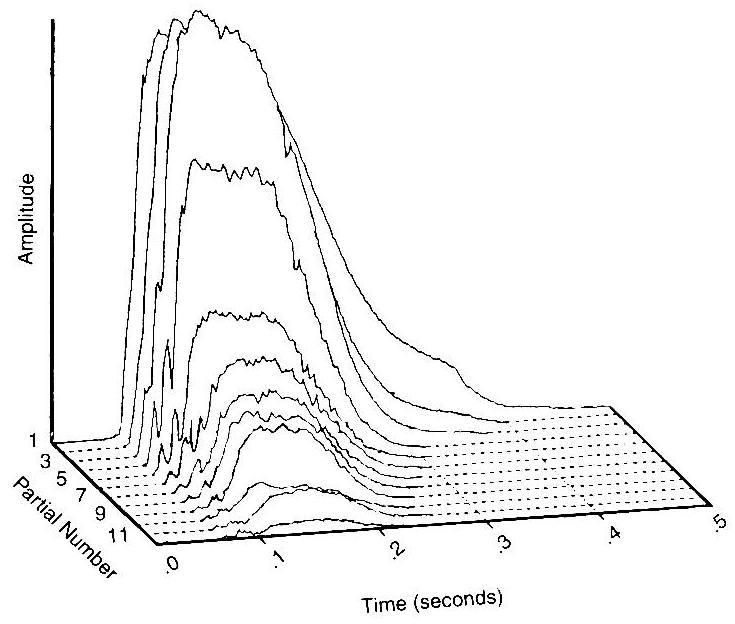
Bild 52: Chronospektrum einer Trompete
Bemerkung: Das sogenannte Powerspektrum ist das Partialton-Spektrum, wo die Quadrate der Amplituden abgetragen werden. Dies macht Sinn, weil diese Grössen die Energien pro Partialschwingung angeben.
Frequenzmodulation
Neben der additiven Synthese, die recht mühsam jede der vielen Partialschwingungen aufbauen muss, gibt es schnellere Verfahren, um den Effekt einer grossen Zahl von Partialschwingungen zu erreichen. Berühmt ist das von John Chowning 1973 publizierte Verfahren der FM- (Frequenz-modulierten) Synthese (oder FM-Analyse). Chowning geht davon aus, die Sinus-Funktionen nicht einfach zu addieren wie Fourier, sondern sie funktionell zu verketten, siehe Bild 53. Siehe Dave Benson's homepage für FM, Musik, Chowning etc.
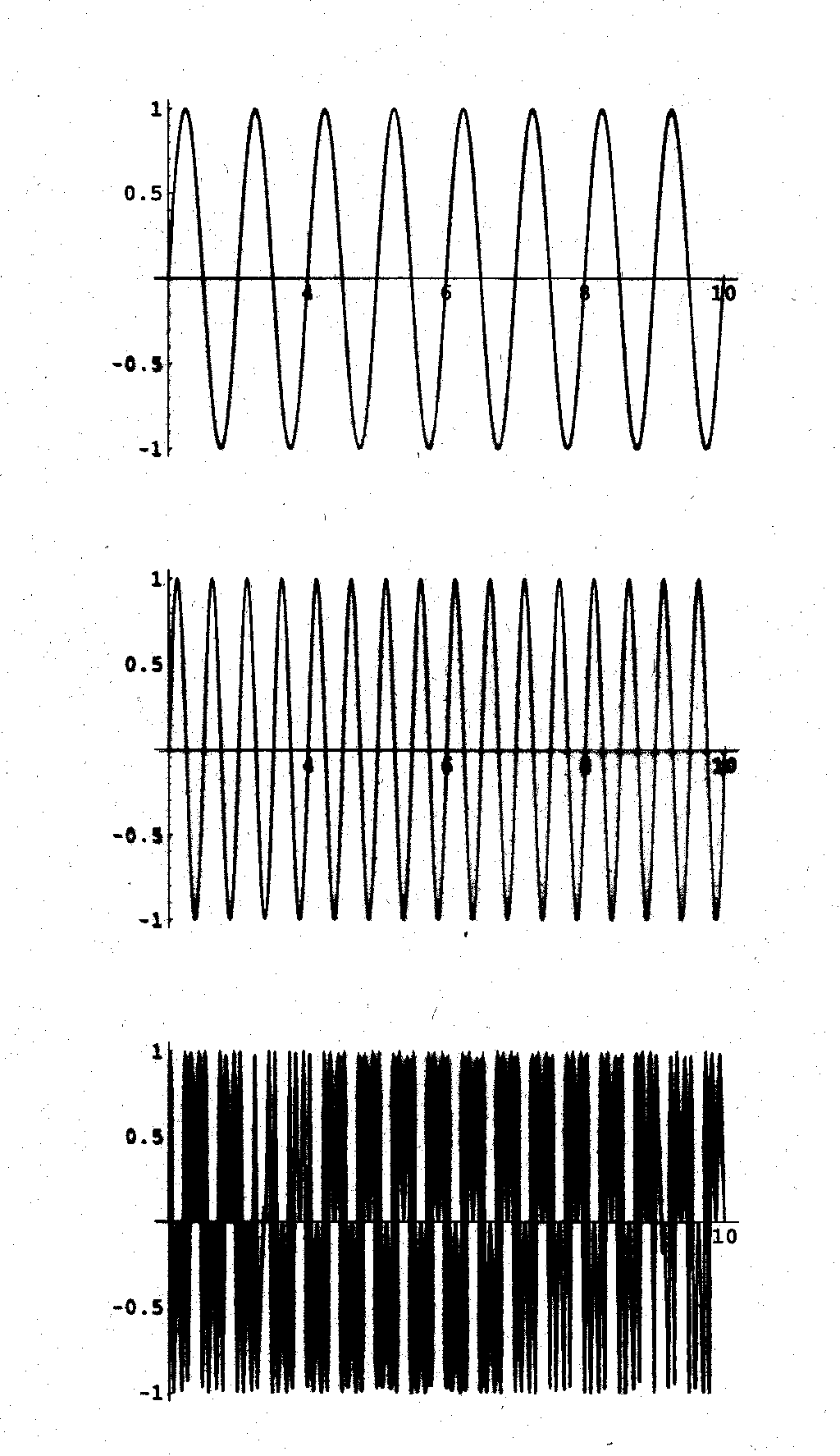
Bild 53: Verkettung von Sinus-Funktionen
Wir sehen zuoberst die Funktion sin(2Pi.t), in der Mitte die Funktion sin(2Pi.2t) und unten die Verkettung sin(2Pi(sin(2Pi.2t))), wo also t in der obersten Sinus-Funktion durch die Sinus-Funktion in der Mitte ersetzt worden ist. Diese Operation führt zum Begriff der Frequenz-Modulation. Wir können damit ein allgemeines Verfahren einleiten. Bild 54 zeigt, was die Idee ist: Wir haben die in Bild 54 durchgeführte Verkettung links oben im Rechteck eingezeichnet. Das Resultat wird nun addiert zu einer anderen Sinus-Funktion, rechts unten im Bild. Das bedeutet, dass man also ganze "Bäume" von Verkettungen und Summationen bilden kann.
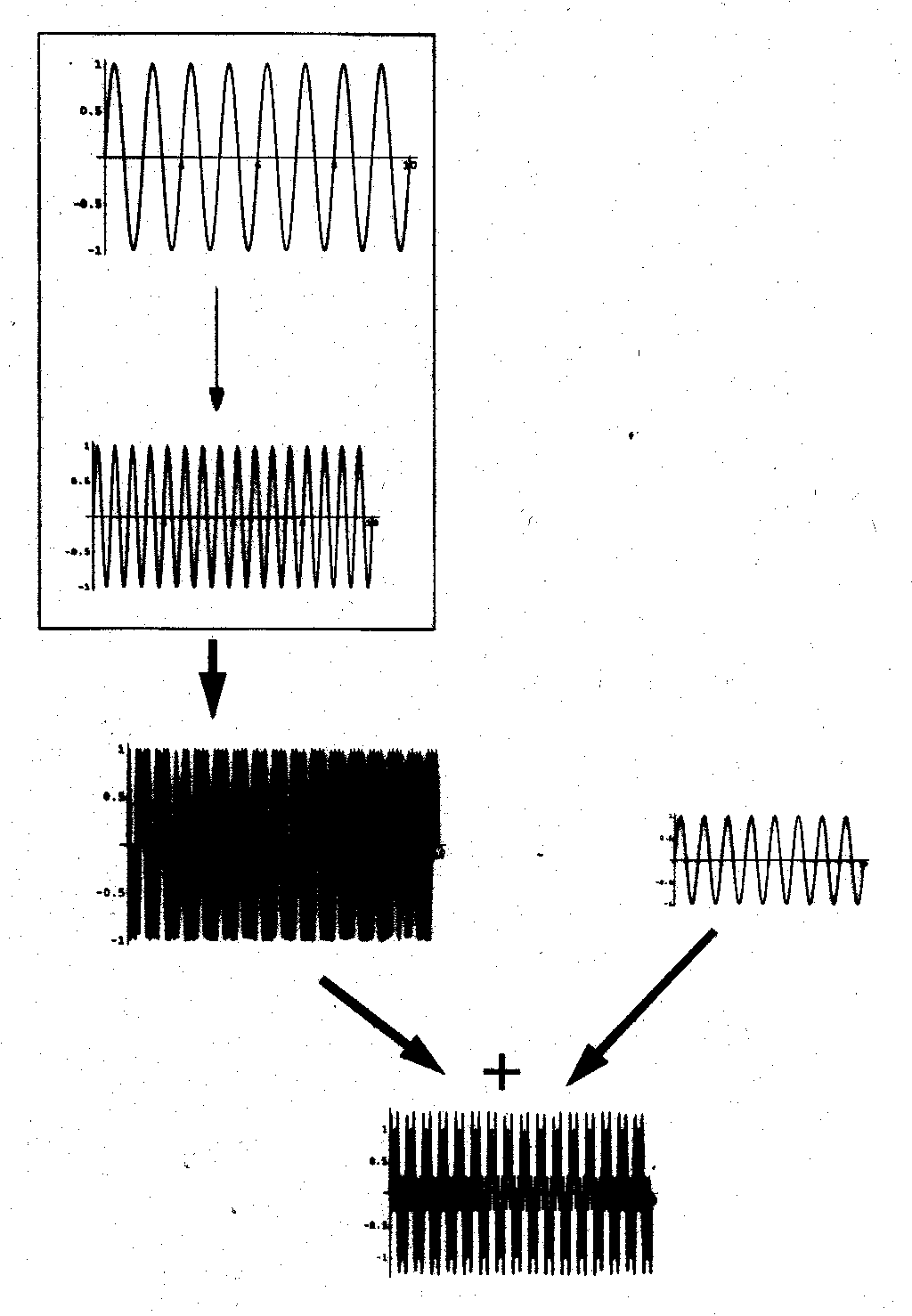
Bild 54: Verkettung und Addition von Sinus-Funktionen
Nach diesen heuristischen Überlegungen wollen wir das Verfahren exakt beschreiben:
- f(t) = Summe von Knotenfunktionen f_i(t)
- Eine Knotenfunktion ist von der Gestalt:
wobei die Funktion, die an der Stelle "Summe... " steht, auch die Nullfunktion sein kann.A.sin(2Pi.Ft + Ph+ Summe von weiteren Knotenfunktionen)
Die in einer Sinus-Funktion dabei auftretende "Summe von weiteren Knotenfunktionen" heisst der Modulator der Knotenfunktion, die Knoten-Sinus-Funktion selber der Träger der Knotenfunktion.
Dieses Verfahren bringt sehr schnell realistische Partialtonverteilungen in der resultierenden Funktion. Die legendäre DX-Familie der Yamaha-Synthesizer benutzt dieses Verfahren mit fünf Knotenfunktionen, siehe Bild 55. Wir sehen drei Exemplare von solchen "Algorithmen" (Terminologie von Yamaha). Man kann hier auch sehen, dass durch Verschwindenlassen gewisser Modulatoren der obere Algorithmus in den linken oder rechten Algorithmus "entarten" kann. So lassen sich ganze Familien von Sounds hierarchisch ordnen.
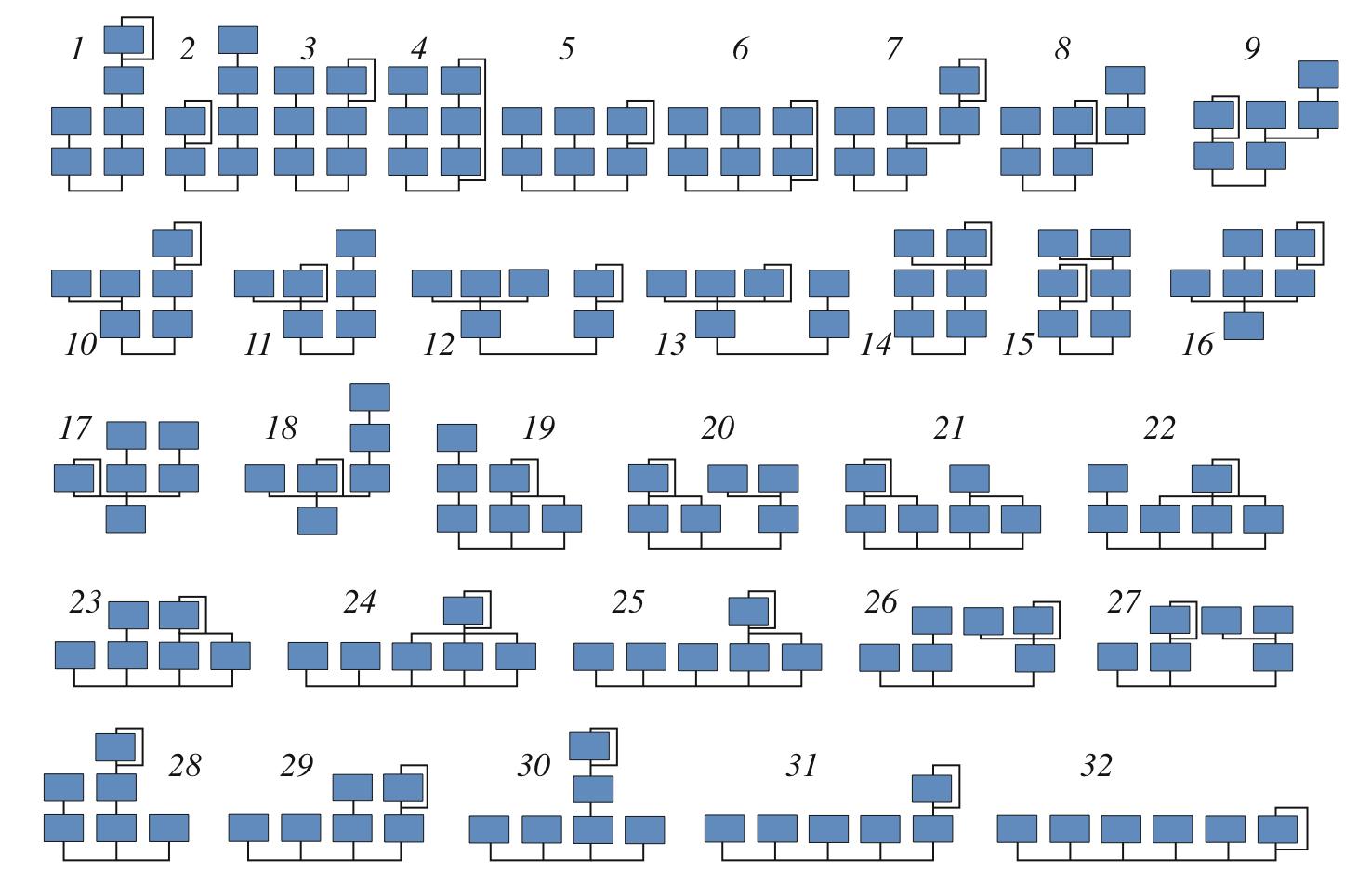
Bild 55a: DX-Familie (Yamaha DX7 Syntesizer) von Algorithmen, deren Knoten-Träger Sinus-Funktionen sind
Bild 55b: Spezialisiserung von entsprechenden Klangfarben zu Algorithmen
Man muss hier allerdings betonen, dass trotz dieser anschaulichen Verknüpfung von Klangfarben die Gesamtheit der Klangfarben weitgehend unverstanden ist, d.h. es gibt keine vernünftige "Geographie der Klangfarben".
Wavelets
Sowohl die Fourier- als auch FM-Darstellung sind grundsätzlich auf unendlich ausgedehnten periodischen trigonometrischen Funktionen aufgebaut und also solche nicht realistisch...
Man hat deshalb auch begonnen, andere "Koordinatenräume" für Schwingungen zu untersuchen und anzuwenden. Wavelets sind eine ganz andere Art von Koordinatenfunktionen, siehe Bild 56. Das Bild zeigt links oben einen Typus (mit entsprechender komplexwertiger Formel
| g(t) = C.exp(-1/2.t^2).exp(iw.t) |
(exp die Exponentialfunktion, im Bild 56 C=1, w=20) von Wavelets, es sind aber viele verschiedene Typen möglich. Wichtig ist, dass es sich immer um "Wellenpakete" handelt, also Funktionen, die nur ganz kurz ausschwingen und dann wieder auf Null gurückgehen.
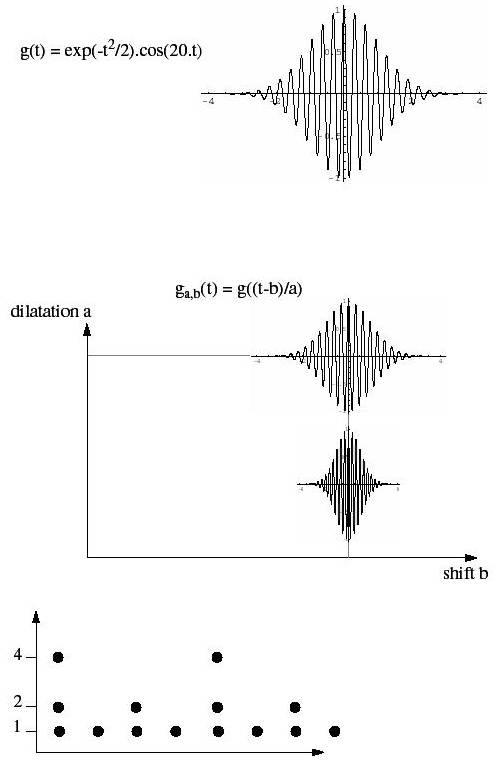
Bild 56:Ein Wavelet und seine Verzerrungen
Æhnlich wie bei der Sinus-Funktion werden auch Wavelets verzerrt. Die Verzerrungsparameter sind zwei Zahlen a und b, und das verzerrte Wavelet g_{a,b}(t) ist in Bild 56, Mitte, angegeben. Man nennt aus naheliegenden Gründen a = Dilatation und b = Shift. Zwei Verzerrungen sind in der Mitte von Bild 56 angegeben.
Die Grundtatsache über Wavelets ist, dass man mit einem Wavelet und seinen Verzerrungen alle Funktionen (solange sie nicht zu wild sind) darstellen kann. Die Details sind in der folgenden Formel abzulesen. Man definiert für jedes Paar (a,b) eine neue Funktion S(b,a) (g*_{a,b} ist die komplex-konjugierte Funktionzu g_{a,b}). Wenn man alle S(b,a) kennt, kann man mit der zweiten Formel die ursprüngliche Funktion wieder erhalten.
| S(b,a)=(1/Wurzel(a))Integral g*_{a,b}(t).s(t)dt und s(t)=Q_g Integral g_{a,b}(t).S(b,a)da db |
Allerdings ist das praktisch nicht brauchbar, da man ja unendlich viele Werte der Hilfsfunktion S(b,a) benötigt. Aber in der Praxis kann man eine geschickte Auswahl von Werten (a,b) nehmen und aus den entsprechenden S(b,a) die urspüngliche Funktion sehr gut approximieren, in der Tat mit viel weniger Aufwand als mit der Fourier-Darstellung. Das Gitter unten in Bild 56 zeigt eine solche Auswahl.
Bild 57 zeigt die Darstellung einer musikalischen Passage mit Wavelet-Darstellung. Die Grauwerte sind proportional zu den Werten S(b,a) für entsprechende Paare (a,b). Die schwarzen Stellen in der Graphik zeigen die Oktavintervalle in der Partitur.
Wie die Fourier- und die FM-Darstellung, so ist auch die Wavelet-Darstellung schon in der Instrumententechnologie angewendet worden.

Bild 57: Darstellung einer musikalischen Passage mit Wavelet-Darstellung
- Masse-Feder-Modelle (mass-spring). Hier werden ganz klassische dynamische Systeme von punktförmigen Massen, die durch Federn verbunden sind und die Physik eines Instrumentes simulieren, nachgerechnet. ZB: Chordis Anima (Institut ACROE, Grenoble, ICMC 1994).
- Modal-Synthese: Man modelliert verschiedene Sinus-Frequenz-Komponenten eines schwingenden Systems und ermittelt experimentell die Parameter, die einem realen Sound entsprechen. ZB. Modalys~Mosaic vom IRCAM (Institut Recherche Coordination Acoustique Musique) durch Jean-Marie Adrien.
- Waveguide: Fortpflanzung von Wellen in einem Medium, zB. Luftsäule in Blasinstrument oder Welle auf Saite. ZB: das Stanford-basierte CCRMA (Center for Computer Research in Music and Acoustics); einer der prominentesten Vertreter des Physical Modeling ist Julius O. Smith; es gibt auch schon kommerzielle Realisierungen in YAMAHA-Synthesizern VL-1.
Wie komplex ein solches Physical-Modeling-System sein kann, zeigt das von P. Cook gebaute Singer-System zur Simulation der menschlichen Stimme, sieheBild 58. Das Singer-System benutzt die Waveguide-Methode. Wir erkennen aber auch darin wieder den aus N-Music stammenden Aufbau aus Einheitsgeneratoren.

