Nach der Übersicht im vorangehenden Kapitel werden wir nun die endliche Fourierzerlegung genauer anschauen und dazu einen schnellen Algorithmus, die Fast Fourier Transform FFT, diskutieren. Wir schliessen das Thema ab mit der Diskussion einer populäre Anwendung davon, dem MP3-Audioformat.

Die detaillierte mathematische Diskussion der endlichen Fourier-Zerlegung kann in der Online-Version des Buches "Comprehensive Mathematics for Computer Scientists" resp. vom entsprechenden Modul "Fourier Theory and Wavelets" im Kurs "Core IT Mathematics" verfolgt werden.

---

Endliche Fourier-Zerlegung "revisited"

Um die mathematische Darstellung auf das Wesentliche zu reduziereen, werden wir hier die Periode T, während der das Signal N mal in Sampleabständen Δ abgetastet wird, normieren zu T = 1, i.e., Δ = 1/N. Wir werden auch die Zeitgrenzen auf das Intervall von 0 bis 1 legen, so dass also die N Zeiten

0/N, 1/N, 2/N, 3/N, ... k/N, (k+1)/N,..., (N-1)/N

abgetastet werden. Ferner wird hier die Fourier-Zerlegung mit der Eulerschen Formel für die Exponentialfunktion exp(ix) = cos(x) +i.sin(x) benutzt (i = Wurzel(-1) die imaginäre Einheit). Man hat statt

f(t) = A_0 + Σ_{n=1,2,3,...} A_n.cos(2Pi.nF.t)+B_n.sin(2Pi.nF.t)

die Darstellung

f(t) = Σ_{n=...-3,-2,-1,0,1,2,3,...} γ_n.exp(i.2Pi.nF.t),

welche durch die Formeln

A_n = γ_n+γ_{-n},

B_n = i(γ_n-γ_{-n})

korreliert sind. Der Ansatz in dieser Schreibweise, welcher der obigen Formel (mit den entsprechenden laufenden Indices)

f(rΔ) = a_0 + 2.Σ_{m=1,2,3,...,n-1} a_m.cos(2Pi.mF.rΔ)+b_m.sin(2Pi.mF.rΔ)+a_n.cos(2Pi.nF.rΔ)

entspricht, lautet mit Δ = 1/N und F = 1, und den neuen laufenden Indices (r—>k, m—>n, n—>N/2)

f_k = f(k/N) = Σ_{n=0,1,2,3,... N-1} γ_n.exp(i.2Pi.n.k/N).

Bemerkung: Beachten Sie dass die Formel 1 = exp(i.2Pi.nF.k/N).exp(i.2Pi.nF.(N-k)/N), und deshalb exp(i.2Pi.nF.(N-k)/N) = exp(i.2Pi.nF.-k/N), zeigt, dass die scheinbar nicht-negativen Indices in der Exponentialdarstellung in Wirklichkeit eine "symmetriesche" Indizierung in positiven und negativen Werten verbirgt. Dies ist wesentlich, um zu verstehen, weshalb reelle Werte von a_n, b_n durch die Werte γ_n möglich sind.

---

Die Geometrie der endlichen Fourier-Zerlegung

Die obigen Funktionen f = (f_0, f_1, f_k,...,f_{N-1}) , welche wir betrachten, bilden den komplexen Vektorraum C^{Z_N}, wobei C = komplexe Zahlen, Z_N = {0, 1, 2,...k,...,N-1}. Auf diesem Vektorraum wird eine Geometrie definiert durch die (sogenannt Hermitesche) Form

<g,h> =1/N. Σ_{k=1,2,3,...,N-1}g_k.h_k^- (^- = komplex-konjugierte Zahl)

(das ist eine Verallgemeinerung der bekannten Euklidischen Geometrie) und die assoziierte Norm (Länge von Vektoren)

||h||^2 = <h,h> = 1/N.Σ_{k=1,2,3,...,N-1}|h_k|^2.

In dieser Geometrie sind die Exponentialfuntionen ausgezeichnet: Setze

e_n(k) = exp(i.2Pi.n.k/N),

dann ist

<e_m,e_l> = 0 für m != l, und <e_m,e_m> = 1.

---

Ein Beispiel zu dieser Zerlegung findet sich in der Online-Version des Buches "Comprehensive Mathematics for Computer Scientists"
(=> Example 182).

---

Wir können nun den FFT-Algorithmus angehen. Dieser Algorithmus wurde in einem kurzen, nur 5 Seiten langen Paper "An Algorithm for the Machine Calculation of Complex Fourier Series," durch James W. Cooley des IBM T.J. Watson Research Center und John W. Tukey von der Princeton University und den AT&T Bell Laboratories publiziert und gehört zu den meist zitierten Resultaten unserer Zeit.

Um dessen Leistung zu verstehen, muss man zuerst ein Mass für die Berechnungskomplexität definieren. Es geht darum, zu beschreiben, was die Anzahl von Rechenoperationen ist, welche nötig sind, um eine Berechnung einer Formel durchzuführen, die von einer Dimensionszahl n abhängt. ZB. soll angegeben werden, wieviele Operationen nötig sind, um zwei nxn-Matrizen zu multiplizieren. Dabei geht es immer um die Frage, wie diese Zahl wächst, wenn in dieser Formel n —> ∞ geht.

Dies ist durch die sogenannten Landau-Symbole formalisiert:

Man betrachtet zwei Folgen c = (c_n)_n und d = (d_n)_n von reellen Zahln c_n, d_n mit natürlichen Indices n = 0,1,2,3,..Dann heisst d von der Ordnung O von c, in Symbolen: d <=_O c, falls es eine positive reelle Zahl λ gibt so dass d_n <= λ c_n ist für hinreichend grosse Indices n. Diese Relation is reflexiv und transitiv, aber nicht antisymmetrisch. Die Ordnung von c ist definiert als die Menge O(c) aller d mit d <=_O c. Die daraus abgeleitete Relation c ~ d <=> d <=_O c & c <=_O d ist eine Äquivalenzrelation, deren Klassen mit Θ(c) notiert werden und Wachstumsklassen heissen. Das heisst also

Θ(c) = Θ(d) genau dann, wenn es zwei positive reelle Zahlen λ, μ gibt mit d_n <= λ c_n und c_n <= μ d_n für hinreichend grosse Indices n.

Die Ordnung vererbt sich offensichtlich auf die Wachstumsklassen. Man hat dann zB. Θ(256.n^2 + 50.n) < Θ(n^3).

Übung: Zeige, dass Θ(n.log(n)) < Θ(p(n)) für jedes Polynom p(n) = a.n^2 +b.n + c mit positivem höchstem Koeffizienten a.

---

Die Wachsumsklasse der endlichen Fourier-Zerlegung

Wieviele arithmetische Operationen sind nötig, um die Koeffizienten

γ_n = <f,e_n> =1/N.Σ_{k=0,1,2,3,... N-1} f_k.exp(-i.2Pi.n.k/N)

zu berechnen? Dazu nehmen wir an, dass die Quantitäten f_0,f_1,...,f_{N-1} und der grundlegende Wert e(N) = exp(i.2Pi.1/N) alle bekannt sind. Um die γ_n zu berechnen, braucht man maximal N-2 Multiplikationen, um e(N)^2, e(N)^3,..., e(N)^{N-1} zu berechnen. Und für jedes n braucht man N Multiplikationen, um die Werte f_k. e(N)^{kn} zu bekommen. Dann noch N-1 Additionen und eine Multiplikation mit 1/N. Das macht q(N) = 2N^2+N arithmetische Operationen, um alle γ_n zu berechnen. Der FFT-Algorithmus ermöglicht es, die Wachstumsklasse Θ(q(N)) auf Θ(log(N)N) zu reduzieren für spezielle Werte der Form N = 2^m. Sei Fourier(N) die Wachstumsklasse der minimalen Anzahl von arithmetischen Operationen (Addition, Multiplikation), um alle γ_n zu berechnen, dann gilt

Θ(Fourier(N)) <= Θ(N.log(N))

Dieser wichtige Satz folgt sofort aus einem Hilfssatz:

In der Tat ist dann induktiv:

Fourier(2N) <= 2Fourier(N) + 8N <= 2N.log(N) + 8N = 2N(log(N)+4) <= 2N(log(2N)).

Der Beweis der Formel Fourier(2N) <= 2Fourier(N) + 8N ist der eigentliche FFT-Algorithmus. Wir führen in deshalb hier aus!

Man hat also die 2N Koeffizienten γ_n von f zu berechnen.

Schritt 1: Unterteilung der Berechnung in zwei halb so grosse Berechnung der je N Koeffizienten von zwei Hilfsfunktionen f⁺ und f^- mit

f⁺_k = f_{2k}, k = 0,1,2,... N-1

f^-_k = f_{2k+1}, k = 0,1,2,... N-1

Die Berechnung der Koeffizienten

γ⁺_0, γ⁺_1,... γ⁺_{N-1} von f⁺ und

γ^-_0, γ^-_1,... γ^-_{N-1} von f^-

hat die Wachstumsklasse 2.Fourier(N). Wenn man γ⁺_{k+N} = γ⁺_k und γ^-_{k+N} = γ^-_k definiert, dann gilt offenbar

γ_k = 1/2.(γ⁺_k +e(2N)^k.γ^-_k), k = 0,1,...2N-1

Also hat man für die Berechnung jedes γ_k drei Operationen: zwei Multiplikationen und eine Addition, ferner für die Berechnung der Potenzen e(2N)^k maximal 2N Muliplikationen. Also insgesamt

3.2N + 2N + 2.Fourier(N) = 2.Fourier(N) + 8N. QED.

Dieses Verfahren ist also rekursiv, man berechnet immer die Hälfte der Koeffizienten, und von diesen auch zweimal die Hälfte, etc. Da wir annehmen, dass N = 2^m, kommt man so bis an den Anfang mit dem Verfahren.

---

Ein Beispiel zum FFT-Algorithmus findet sich in der Online-Version des Buches "Comprehensive Mathematics for Computer Scientists"
(=> Example 183).

---

---

Das MP3-Audio-Format

Zur Terminologie und Geschichte

MPEG (Moving Pictures Experts Group) ist der Codename für die Standardisierungruppe ISO/IEC JTC1/SC29/WG11 (Int. Standards Organization/Int. Electrotechnical Commission) und wurde 1988 ins Leben gerufen, um generische Standards für kodierte Darstellung von digitalen Video- und insbesondere Audio-Daten zu entwickeln.

MPEG-1 ist das Resultat der ersten Arbeitsphase der Gruppe und wurde 1992 als ISO/IEC IS 11172 verabschiedet. Es enthält Layer-1, Layer-2, Layer-3, d.h., drei Operationmodes mit wachsender Komplexität. Unter MP3 versteht man den Layer 3 von MPEG-1.

MPEG-2 Advanced Audio Coding (AAC) ist das Resultat der zweiten Arbeitsphase. Es verbessert die Layer-3 in vielen Details. Wir diskutieren diese Variante hier nicht.

Die Entwicklung dieser komprimierten Audioformate geht auf die Arbeiten von Dieter Seitzer seit 1960, damals bei IBM und seines Schülers Karlheinz Brandenburg, der vor allem für die psychoakustischen Kompressionsmethoden verantwortlich ist. Interessanterweise wurde Seitzers Patent 1977 noch abgelehnt, 1983 schliesslich doch noch erteilt, aber wegen Desinteresse der Industrie dann fallen gelassen. MP3 geht vor allem auf die Forschung und Entwicklung unter Karlheinz Brandenburg am Fraunhofer Institut für Integrierte Schaltungen (IIS) in Erlangen zurück. Es ist ein offener Standard, wird aber durch zahlreiche Patente (>=13 US-Patente, >=16 deutsche Patente) geschützt, siehe unten für die rechtlichen Aspekte.

MP3 schliesst Optionen ein wie

• Mono und Stereo, insbesondere Joint stereo encoding für effiziente kombinierte Kodierung der beiden Kanäle
• Samplingfrequenzen schliessen 32 kHz, 44.1 kHz, 48 kHz ein, für MPEG-2 auch 16 kHz, 22.05 kHz, 24 kHz und für MPEG-2.5 (Fh-interne Erweiterung) auch 8 kHz, 11.05 kHz, 12 kHz.
• Die Bitrate der Kompression (also die Bits, welche pro Sekunde durch das komprimierte Audiofile laufen) ist von 32 kbits/s (MPEG-1) resp. 8 kbits/s (MPEG-2) bis 320 kbits/s. Die Bitrate kann für MP3 sogar von Frame zu Frame (das ist das Einheitspaket im Datenformat von MP3) variieren und erlaubt zusammen mit der sog. Bit-Reservoir-Technologie eine variable und fixe Bitrate.

Ich verweise zum Thema MP3 auch auf die Diplomarbeit "Das neue Audiospeicherformat MP3" von Pascal Schriber am IFI. Dort finden sich auch viele weitere Internet-Quellen

---

Die Kodierungskette

Bild 58b1 zeigt die Originalgraphik der Kodierungs-Kette in Brandenburgs Publikation.

Bild 58b1: Die MP3-Kodierungskette nach Brandenburg

Die Kodierkette umfasst im wesentlichen fünf Komponenten:

1. Digitaler Audiostream
2. FFT mit Filterbank
3. Psychoakustisches Modell PAC
4. Quantisierung
5. Huffman-Kompression

Der Richtwert der Kompression durch diese Kette ist 1:12, obwohl die Kompression natürlich stark variiert werden kann je nach Bedarf.

Diese Kette komprimiert verlustbehaftet (lossy), und zwar nicht im Huffman-Teil 5, sondern durch die PAC-Kompression 3 und die Quantisierung 4.

Wir verzichten hier auf die Beschreibung der Dekodierkette, welche im wesentlichen zur Kodierkette symmetrisch verläuft.

---

FFT mit Filterbank

Zunächst beachte man zur FFT, dass selbstverständlich bei endlicher Fourier-Zerlegung die Zahl N der Zeit-Samples f_0,f_1,... f_{N-1} immer gleich gross ist wie die Zahl der Koeffizienten γ_0, γ_1,... γ_{N-1}. Letztere bezeichnet man auch als Frequenz-Samples. Dies ist wichtig, wenn man die Kompression berechnet, da im Fall, wo beide Samples mit derselben Bit-Auflösung (16 bit in unserem Fall) gesetzt werden, der Input Zeit-Samples, der Output für die Kompression aber Frequenz-Samples meint. Da die Zahlen aber übereinstimmen, lassen sich diese beiden Sample-Typen aber für diesen Zweck "identifizieren".

Die Filterbank für layer-3 ist eine "hybride" Filterbank. Es werden für ein gegebenes Zeitfenster (rund 1/40 Sekunde, s.u.) in einer ersten Stufe eine "polyphase" Filterbank zu 32 Frequenzbändern erstellt. Diese sind auch schon in Layer-1 und Layer-2 vorhanden und alle von der Breite von 625 Hz (d.h. insgesamt eine Frequenzbreite von 0-20 kHz). Bei Layer-3 dann sind die Bänder von variabler Breite und es wird jedes der 32 Bänder noch in 18 Subbänder unterteilt. Die Bänder sind am schmalsten in dem für das menschliche Ohr sensibelsten Bereich zwischen 2 und 4 kHz. Die zusätzliche Fourieranalyse dazu heisst MDCT (=Modified Discrete Cosine Transformation), sie ist eine Variante der endlichen (diskreten) Fourier-Zerlegung, benutzt nur Cosinusfunktionen. Sie hat den Vorteil, gewisse Artefakte der Überlappung von Subbändern aufzufangen; wir gehen darauf nicht ein.

---

Das Perceptual-Audio-Coding-Modell (PAC)

Das PAC ist das Herzstück von MP3. Es setzt dort ein, wo die rein mathematischen Analysen nicht greifen: in der psycho-physiologischen Wahrnehmung von Klängen. Das PAC-Modell geht davon aus, dass drei Beschränkungen im Hörvermögen des Menschen zwischen den bekannten Grenzen von 16 Hz bis 20 kHz existieren:

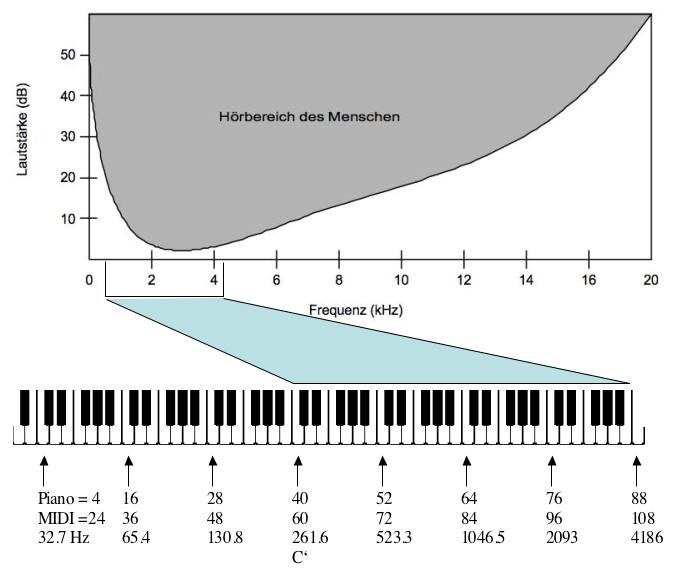
PAC 1: Schwellenwerte im Hörbereich des Menschen

Sinustöne einer bestimmten Frequenz F Hz werden vom Menschen nur über einer minimalen Lautstärke S(F) dB gehört. Die Kurve der Hörschwellen ist in Bild 58b2 ersichtlich.

Bild 58b2: Hörschwellenkurve des Menschen als Funktion der Frequenz, darunter zum Vergleich eine Klaviertastatur

Man erkennt darin die maximale Sensibilität im Bereich zwischen 2 und 4 kHz, darunter ist zum Vergleich eine Klaviertastatur angezeigt. Unterhalb der Hörschwellenkurve wird ein Sinuston nicht gehört. Wenn man also in der Fourier-Zerlegung Sinuskomponenten unterhalb der Schwelle erhält, können diese weggelassen werden. Von den 65'536 Werten der 16-bit-Darstellung der Teiltonamplituden müssen also viele Werte erst gar nicht gespeichert werden.

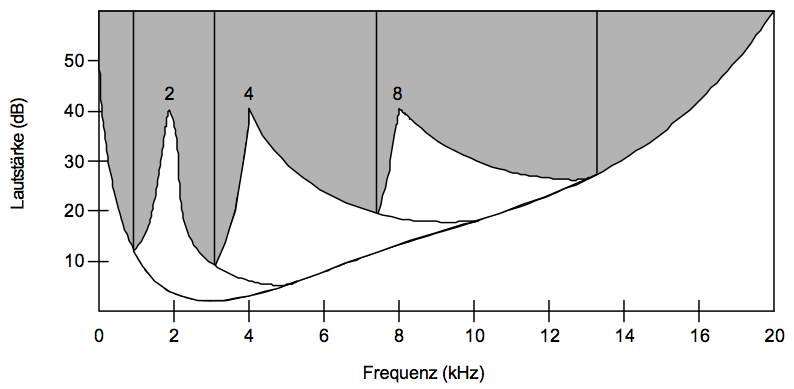
PAC 2: Maskierung im Frequenzbereich

Bild 58b3: Maskierung im Frequenzbereich

Im Frequenzbereich existiert ein Maskierungseffekt, bei dem für das Auftreten einer Komponente einer bestimmten Frequenz andere benachbarte Komponenten nicht hörbar sind, wenn sie unter die Maskierungskurve dieser Frequenz fallen. Bild 58b3 zeigt für drei Frequenzen 2,4,8 kHz und eine Lautstärke von 40 dB die entsprechenden Maskierungen. Dadurch kann man alles, was unterhalb dieser Kurven liegt, weglassen. Man muss nun entsprechende Schlüsselfrequenzen und deren Überdeckungskurven auswählen, welche für ein gegebenes Spektrum über andere "dominieren".

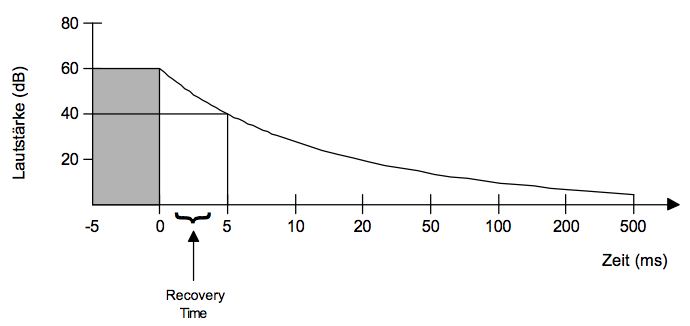
PAC 3: Maskierung im Zeitbereich

Bild 58b4: Zeitliche Maskierung durch Erholungszeit nach einem 60 dB Signal

Nach einem Signal einer bestimmten Lautstärke ist das Hörsystem nicht sofort imstand, andere Signale zu verarbeiten, deren Lautstärke kleiner ist als die gegebene; das System muss sich erst "erholen". Die Sensibilität als Funktion der Zeit nach dem Anfansgssignal ist in Bild 58b4 angegeben. ZB. wird also nach 5 ms ein anderes Signal mindestens 40 dB haben müssen, um wahrgenommen zu werden. Eine Erholungszeit (recovery time) zwischen 5 und 20 ms ist ein guter Richtwert. Noch dramatischer ist die Tatsache, dass auch kurz vor einem lauten Ton andere leisere Töne nicht mehr wahrgenommen werden. Dies ist so, weil auch der Aufbau der Wahrnehmung eines Signal eine gewisse Zeit beansprucht.

Insgesamt wird durch die Kompression, welche diese drei Effekte ermöglichen 60% der finalen Kompression geleistet.

---

Quantisierung und Huffman-Kodierung

Nach der Kompression durch die hörpsychologischen und und hörphysiologischen Methoden wird der Datenstrom noch quantisiert und Huffman-komprimiert. Wir wollen das hier nicht im Detail ansprechen, weil es nicht der Punkt dieses Verfahrens ist.

Für die Quantisierung wird beispielsweise Bitallokation durchgeführt, was heisst, dass beispielsweise bei der 16-Bitdarstellung 1101'1100'1011'0101 die kleinsten fünf Bits annulliert werden, also 1101'1100'1010'0000 entsteht. Man behält dann davon die elf nicht korrigierten Bits 1101'1100'101 und die Verschiebung (Skalierung) um 5 Bits.

Bevor die Huffman-Kodierung angewendet wird, lässt das Verfahren noch eine (verlustfreie) Lauflängenkodierung laufen, wobei bekanntlich die Wiederholung von Zeichen durch das einmalige Auflisten der Zeichen plus die Notation der Wiederholungsrate ersetzt wird. Auch die nachfolgende Huffman-Kompression ist verlustfrei und kodiert die häufigsten Frequenzen durch kürzeste und die seltensten Frequenzen mit den längsten Bitsequenzen nach dem bekannten Verfahren der (meist binären, hier allerdings quaternären) Huffman-Bäume.

---

Das Datenformat

Das Datenformat, sowohl für die Streaming-Repräsentation als auch für die Speicherung von MP3-Daten, besteht aus einer Reihung von Frames. Frames sind Informationseinheiten, die neben den reinen Audiodaten auch Hilfsdaten enthalten und so das Frame als praktisch autonome Informationsquantität gestalten. Das heisst, dass die Kodierungsdaten pro Frame mitgeliefert werden, so dass das Abspielen einer MP3-Datei mitten im Musikstück beginnen kann. Ein Frame dauert rund eine 40stel Sekunde, so dass also diese Frame-Zerlegung für den Menschen praktisch nahtloses Abspielen ermöglicht. Bild 58b5 zeigt eine Framesequenz.

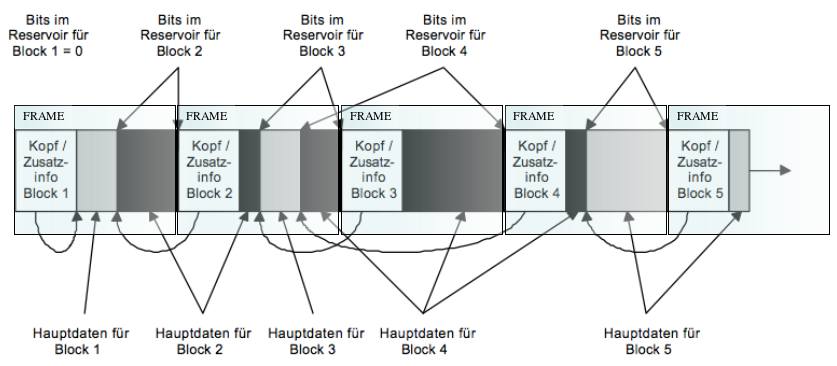
Bild 58b5: Ausschnitt aus der Frame-Sequenz des MP3-Datenformats.

Ein Frame hat

• einen 32-Bit langen Header, welcher die Layer-Nummer (1-3), die Bitrate und die Abtastfrequenz enthält;
• den Cyclic Redundancy Check (CRC) mit entweder 0 oder 16 Bits für Fehlerentdeckung (Prüfsummencheck), allerdings ohne Korrekturmöglichkeit, aber evtl. Framerepetition bis ein intaktes Frame kommt;
• 12-Bit für Zusatzinfos für Huffman-Bäume und Bitallokation-Skalierung
• Hauptdaten-Sampleblock zu 3344 Bits für die Huffman-kodierten Frequenzsampledaten.

Am Ende der gesamten MP3-Datei ist ein 128-Byte-Identifikator ein "ID3-Tag" angefügt, der allerdigs kein offizieller Standard ist, aber für viele Infos über Musik wesentlich. Hier seine Aufgliederung:

Bytes	Inhalt
3	Tag = Kennung des ID3-Tags
30	Titel des Stücks
30	Name Interpret
30	Name Album
4	Jahr Publikation
30	Kommentar
1	Genre-Kennung

Da die Sample-Zahlen für Zeit- und Frequenzsamples gleich sein müssen (s.o.!), erhalten wir die Gleichung

38.28125 Frame/sec =	44'100 (Zeit-)Sample/sec	=	128 kbit/sec
	1'152 (Frequenz-)Sample/Frame		3.344 kbit/Frame

---

Stereo-Kodierung

Layer-3 implementiert das Kompressionsverfahren Joint Stereo Coding Methods. Dies beruht auf einer Kombnation von zwei Prinzipien:

• dem Midi/Side Stereo Coding (MSSC), wobei man statt der Kanal-Paare (L, R) die gleichwertigen Paare (L+R, L-R) nimmt und dabei ausnutzt, dass die Kanäle L, R meist stark korreliert sind, also nicht zufällige unabhängige Signale beinhalten, und
• dem Intensity Stereo Coding (ISC), wird die Summe L+R und die Richtung, woher das Signal herkommt, kodiert.

---

Performance

MPEG-Verfahren	Kompressionsrate	Musikqualität	Bitrate kbit/sec	Bandbreite kHz	Modus
MPEG-1 Layer-3	14:1 - 12:1	CD	128	> 15	Stereo
MPEG-1 Layer-3	16:1	Annähernd CD	96-112	15	Stereo
MPEG-2 Layer-3	16:1-24:1	Radioqualität	56-64	11	Stereo
MPEG-2 Layer-3	24:1	Sprache	32	7.5	Mono
MPEG-2 Layer-3	48:1	Kurzwellenradio	16	4.5	Mono
MPEG-2.5 Layer-3	96:1	Telefon	8	2.5	Mono

---

Rechtliche Aspekte

Zu den Details dieser Aspekte verweisen wir auf die Quellen und Informationen in der schon erwähnten Diplomarbeit "Das neue Audiospeicherformat MP3" von Pascal Schriber.

Die Lizenzierungsrechte des Fraunhofer IIS werden von der Firma Thomson Multimedia vertreten.

Fraunhofer verlangt an Lizenzen gegenwärtig

0.5 USD pro Decoder

5.- USD pro Encoder

15'000.- USD jährlichen Pauschalbeitrag.

Das heisst, dass ein Unternehmen, das mit einer Total-Auflage von 25'000 Stück Encoder-Software verkauft, im ersten Jahr 25'000 x 5 + 15'000.- = 140'000.- USD , und nachfolgend 15'000.- jährlich an MP3-Lizenzen bezahlen muss.

---