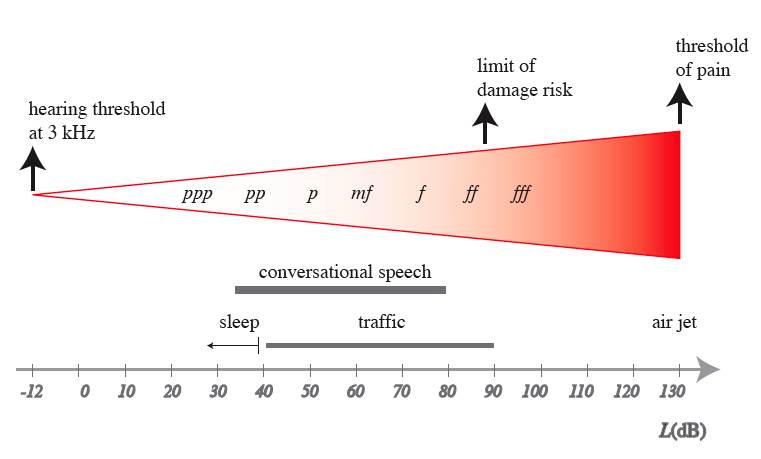
Auf der neutralen Ebene ist das Werk akustisch eine einzige Luftschwingung. Eine CD oder LP etc. ist lediglich eine digitale oder analoge Spur dieser einen Schwingung. Bild 26 zeigt das Prinzip der Digitalisierung. Wir gehen aus von einer Originalschwingung (a) links oben. Diese Schwingung wird in kurzen Zeitabständen abgetastet, die Zeit wird damit quantisiert. Bei CDs ist das aus Gründen, die wir noch im Kapitel über Fourier-Zerlegung diskutieren werden, 44'100 mal pro Sekunde abgetastet.
Zugleich wird auch der Wertebereich der Schwingungsauslenkungen quantisiert. Rechts im Bild sehen wir zwei solche Quantisierungen. Die 1-Bit-Quantisierung gibt uns lediglich zwei approximierte Werte: 0 oder 1, je nachdem, ob der Schwingungswert Null oder nicht Null ist. Die darunter abgebildete 4-Bit-Quantisierung hat 2^4 = 16 Werte zwischen 0 und 15, wobei die Bezeichnung mit den Bits daher kommt, dass man hier mit vier Angaben von Null oder Eins 16 Möglichkeiten hat zu wählen: (0,0,0,0), (0,0,0,1), ..., (1,1,1,1).
Für die Audio-CD benutzt man 16 Bit Quantisierung, das ergibt eine Feinheit von 2 ^16 = 65'536 Werten.Achtung! Diese Digitalisierung hat gar nichts mit der digitalen Datenübertragung etwa von MIDI zu tun! NICHT ALLE DIGITALISIERUNGEN SIND VERTRAEGLICH, Digitalisierung ist semiotisch gesehen nur eine mathematische Ausdrucksweise, der Inhalt ist dabei vollkommen unbestimmt.
Poietisch/aesthesisch wird das akustische Werk, das ja als Ganzes auf der neutralen Ebene eine einzige Luftschwingung ist, als Liste von Sound-Events aufgebaut/zerlegt. Dabei ist das Zerlegen alles andere als klar oder eindeutig, sowohl hörphysiologisch als auch technologisch!
Wir nehmen der Einfachheit halber an, es sei uns gelungen, ein einziges Sound-Event zu isolieren, zum Beispiel ein gewohntes Sound-Event, etwa von Klavier. Wir haben also eine kurzfristige Auslenkung x(t) des Luftdrucks vor uns, die von der Zeit t abhängt. Auch hier ist eine neutrale Beschreibung, d.h. eine Beschreibung, die nicht auf einer Konstruktionsvorschrift beruht, nicht eindeutig.
Bemerkung zur Sprache: Die vielen englischen Ausdrücke kommen daher, dass die wichtigen Beiträge heute meist englisch formuliert sind, wir übernehmen das zum Wohle der Studierenden!
Das Sound-Event x(t), welches unten im Bild 27 zu sehen ist, ist ein kurzlebiges Wellenpaket, welches wir wie folgt erhalten. Zunächst gibt man eine Wave W_f (t), welche eine periodische Funktion der Zeit ist, d.h. es gibt eine Zeit-Periode P so, dass immer W_f (t+P) = W_f (t). Die Wiederholungsrate f = 1/P heisst die Frequenz der Wave. Eine Standarddarstellung der Wave benützt die sogenannte Fourier-Zerlegung in Sinus-Funktionen. Wir haben diese in Bild 27 angedeutet:
Später kommen wir auf diese Darstellung periodischer Waves genauer zu sprechen.
Als Zweites geben wir eine Hüllfunktion oder Envelope H(t) an; sie wird bestimmen, in welchem Mass das Sound-Event an- und abschwillt in den zugelassenen Höchstwerten. Die Envelope H ist eine normierte Funktion, welche zwischen t = 0 und t = 1 positive Werte hat, auf einen Maximalwert = 1 anschwillt und vorher und nachher = 0 ist; siehe Bild 27, Mitte.
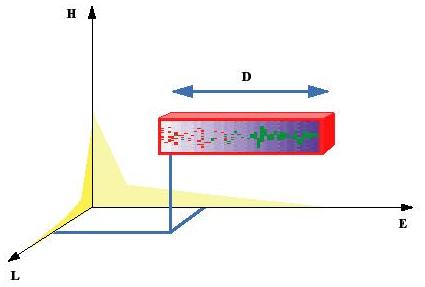
Aus H bilden wir sodann die wirkliche Hüllkurve, welche die Grenzen des Sound-Events bestimmt. Das Sound-Event soll zur Einsatzzeit e (Sekunden) beginnen und eine Dauer von d (Sekunden) haben, also nach e+d (Sekunden) beendet sein. Wir wollen, dass die Schallschwingung eine maximale Amplitude A (Auslenkung vom Normalluftdruck) habe. Das Tripel S = (e,d,A) heisst Support (Träger) des Sound-Events, und die durch S definierte wirkliche Hüllkurve ist
siehe Bild 27, Mitte. Mit diesen Vorgaben erhalten wir das Wellenpaket
Die Zeitfunktion x hängt also von den Parametern (e,f,A,d;H,W) ab. Dabei heissen e,f,A,d die geometrischen Parameter, weil sie das Sound-Event in einem geometrischen Raum darzustellen erlauben (siehe unten), währenddessen der Parametersatz F = (H,W) Farbparameter heisst, da er die Klangfarbe des Events beschreibt.
Um der Art und Weise, wie der Mensch diese Gegebenheiten hört, gerecht zu werden, ersetzt man in der musikalischen Akustik die geometrischen Parameter durch gleichwertige Grössen wie folgt:
Wir haben also das Sound-Event x(e,h,l,d;F)(t) (wobei e, h, l, d wieder geometrische Parameter heissen). Es soll nochmals betont werden, dass diese Darstellung eines Sound-Events massiv poietisch ist, da ausser dem Träger S = (e,d,l) praktisch nichts neutral ist! Dies ist also nicht das Event x, sondern es ist eine (zwar konventionelle) Darstellung der Art, wie das x hergestellt wird. Wir werden später noch ganz andere Herstellungsarten kennenlernen. Damit man sagen könnte, diese Herstellungsparameter seien erkennbar, müsste man ein physikalisches Detektorsystem zur Verfügung haben, welches die Parameter aus x "extrahieren" kann. Ohne hier auf die Hörphysiologie einzugehen möchten wir aber festhalten, dass dies im Falle des menschlichen Gehörs durchaus ein ungelöstes Problem ist.
Wenn wir die physikalische Herstellungsweise eines Sound-Events wie oben voraussetzen, kann man verstehen, wie ein Objekt auf der mentalen Realitätsebene der Partitur als Note beschrieben wird. Wir möchten hier aber vorwegnehmen, dass damit auch das geistige Verständnis der musikalischen Objekte in Komposition und Theorie mitbestimmt wird, dass also eine andere Darstellung auch den kompositorischen und theoretischen Zugang modifizieren könnte.
Eine in der Partitur gesetzte Note X wird beim Performen, also der Aufführungsinterpretation, auf ein Sound-Event abgebildet P(X) = x, P = Performance-Transformation. Man muss also die Parameter von x auf der mentalen Ebene kodieren. Wir können das so schreiben:
X = PianoNote(E,H,L,D), siehe Bild 28 für die Darstellung von X als Pianola-Balken. Die geometrischen Parameter erkennt man als geometrische Ausdehnungen des Balkens, die Dauer ist die Länge des Balkens. Die Klangfarbe zum Namen "PianoNote" haben wir als Textur des Pianolabalkens dargestellt.
Dabei sind E,H,L,D reele Zahlen (= Dezimalbrüche), und der Name "PianoNote" ist ein Wort (für Informatiker: Character String), der auf das Instrument verweist. Wir haben auf der mentalen (= geistigen) Ebene

Man sollte sich aber hüten, die mentale Tonhöhe mit der physikalischen Tonhöhe zu identifizieren, sie ist lediglich eine geistige Grösse, die erst durch die Performance in ein physikalisches Objekt verwandelt wird. Dito für die anderen mentalen Parameter!
Ein interessantes und schwieriges Beispiel der Performance-Transformation ist die Tonhöhe. Wohin wird die mentale Tonhöhe abgebildet?
Dies ist alles andere als trivial, hier erfordert das Musikdenken eine durchaus entwickelte Mathematik zur Beschreibung seiner Objekte. Der Raum der physikalischen Höhen, also h, ist in der Musik streng besetzt. Man betrachtet hier den Eulerraum Eu aller rationalen Kombinationen
h = h(o,q,t)= o.log(2)+q.log(3)+t.log(5)+b = log (f),
im Tonhöhenraum h(R), d.h., o, q und t sind rationale Zahlen (= Quotienten zweier ganzen Zahlen, wie etwa -34/13; Wurzel(2) wäre also verboten). Dies entspricht den Frequenzen
f(h)= B.2^o .3^q .5^t , mit der Bezugsfrequenz B = 10^b .
Damit kann man also alle Frequenzen der klassischen Stimmungen darstellen, wobei 2 -> Oktav, 3 -> Quint, 5 -> Terz erzeugen. Man kann zeigen (durch Benutzung der eindeutigen Primzerlegung für natürliche Zahlen), dass jede solche Tonhöhe durch genau ein solches rationales Tripel (o,q,t) geschrieben werden kann. Wenn wir also mit Eu(Q^3) den Raum aller rationalen Tripel (o,q,t) bezeichnen (dies ist ein dreidimensionaler Vektorraum über den rationalen Zahlen Q), dann haben wir mit der obigen Notation eine (affine) Abbildung
Eu(Q^3) —> h(R): (o,q,t) ~> h(o,q,t),
die es ermöglicht die interessierenden Tonhöhen mit den Punkten von Eu(Q^3) zu identifizieren: Jede erlaubte Tonhöhe entspricht genau einem Punkt (o,q,t). Der Raum Eu(Q^3) heisst der Eulerraum (zur Oktav, Quint und Terz), siehe Bild 32.

Bemerkung zur Normierung: Wenn man ferner fordert, dass der Kammerton a' ~ log(440) als log von 9/12 einer wohltemperierten Oktave drin ist, dh. 440 =B. 2^o.3 ^q.5^t , und dass das c' der wohltemperierte Ursprung ist, dann erhält man
B = 440.2 ^-3/4 oder b = log(440)-3.log(2)/4.
Die Tonhöhen reiner Stimmung sind durch das Gitter Eu(Z^3) der ganzzahligen Tripel beschrieben. Einige dieser Punkte sind in Bild 32 eingezeichnet. Andererseits sind die Tonhöhen der 12-temperierten Stimmung grad die Punkte auf der Geraden durch c' und c'', welche ganzzahlige Vielfache des 12-temperierten Halbtonschritts (1/12,0,0) sind.
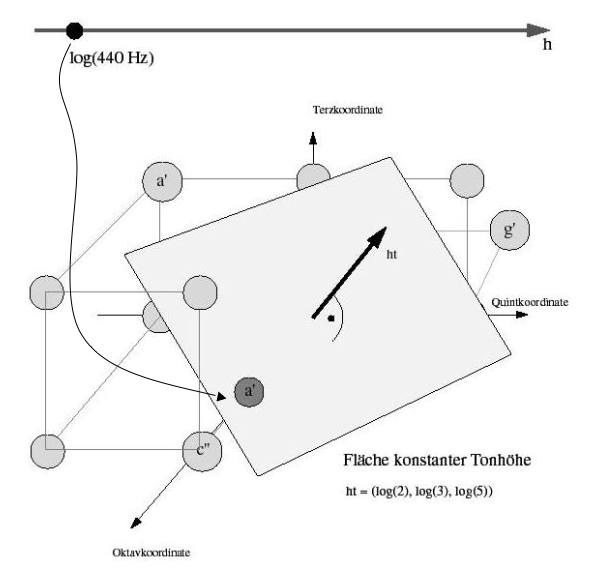
Interessant ist die Darstellung aller Punkte, die eine bestimmte Tonhöhe darstellen: Bild 33 zeigt die Fläche aller Punkte konstanter Tonhöhe. Dramatisch daran ist die Tatsache, dass in beliebiger Nähe jeder solchen Fläche unendlich viele Punkte des Gitters Eu(Z^3) der reinen Stimmung liegen. Mit anderen Worten: Reine Stimmung ist beliebig vieldeutig, auch wenn man beliebig genaue Hörfähigkeit voraussetzt. Die Eulersche Theorie des Zurechthörens ist also gelinde gesagt fragwürdig.
PianoNote (E,H,L,D)
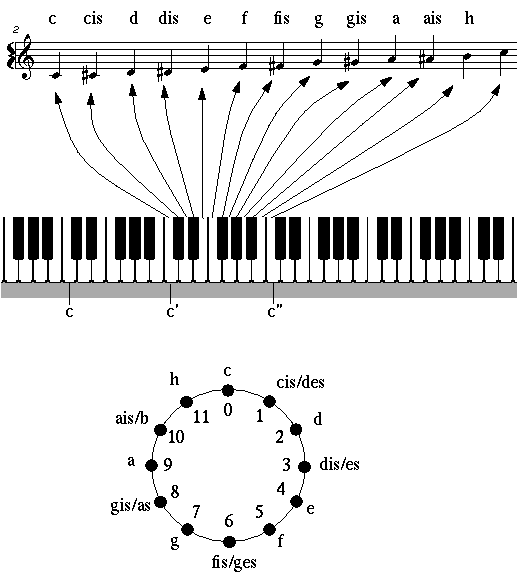
kennengelernt. Hier waren die Wertebereiche für alle Koordinaten die Menge R der reellen Zahlen (Dezimalbrüche), und wir können diese Struktur als E(R) schreiben.Man kann aber auch andere als reelle Werte zulassen, etwa die Menge ASCII der Wörter (Character Strings, ASCII ist das Kürzel des Buchstaben-Codes der amerikanischen Standard-Organisation) oder die Menge Z der ganze Zahlen, usf. Man würde dann z.B. schreiben L(ASCII) für Lautstärken, die als Wörter (wie mf, pp) angegeben sind, oder H(Z) für Tonhöhen, die als ganze Zahlen angegeben sind (wie für Tastennummern eines Klaviers, siehe oben Bild 29). Wir sprechen später über die grundsätzlich möglichen Bereiche.
Man kann andererseits zur Beschreibung musikalischer Objekte auch mehr Parameter einbauen, etwa für Crescendo oder Glissando. Oder weniger Parameter für Pausen oder Taktstriche:
Für den Moment sind die systematischen Fragen nicht wichtig, sondern nur das prinzipielle Vorgehen, wir kommen später darauf zu sprechen.
Man benötigt für Komposition und Analyse aber auch Mengen von Objekten, zB. Akkorde oder Motive. Bild 34 zeigt einen Partiturausschnitt, in welchen man diverse "lokale Karten" für Motive, Akkorde etc. erkennt. Diese Objekte sind also durchaus Standard in Komposition und Analyse. Wie sollen wir sie definieren?
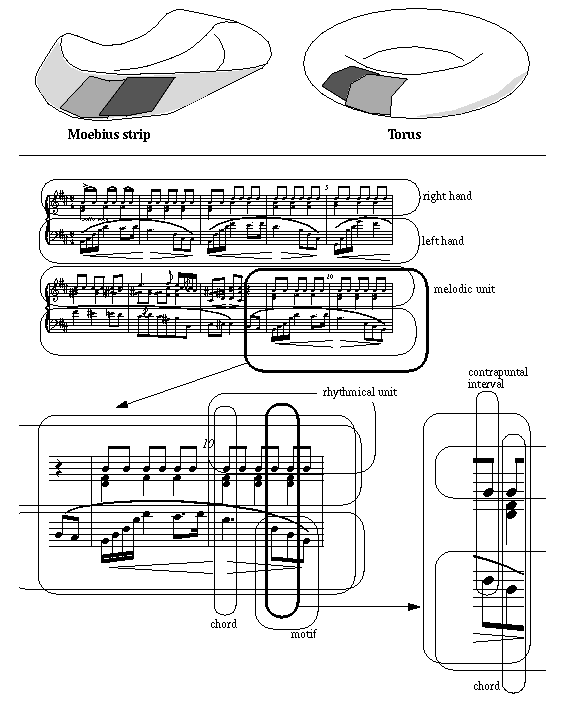
Einen Akkord in einer Klavierpartitur kann man als Menge von PianoNote-Objekten darstellen, mit diesem Symbol: Akkord{PianoNote}, womit wir sagen: Der Objekttyp "Akkord" besteht aus Mengen (geschweifte Klammer {...}) von Objekten des Typs PianoNote, den wir schon kennen. Ein einzelner Akkord wäre dann zu schreiben als
wobei X_1,X_2,...,X_n die Noten des Akkordes A sind. Wir müssen dazu aber eine Nebenbedingung erfüllen: dass nämlich alle Einsatzzeiten dieser Noten gleich sind, d.h. E(X_i) = E = const. für alle i = 1,2,...,n.
eine alternative Definition wäre
Akkord(E, Einsatzgruppe{Note(H,L,D)})
wo wir dann nur eine Einsatzzeit hätten und dafür Mengen von abstrakteren Dingen, die wir "Note" nennen, und die nur die drei Koordinaten H, L, und D hätten. Und so fort.
Mengen von PianoNoten sind natürlich grundsätzlich sehr wichtig für allerlei Begriffsbildungen:
Also könnte man zuerst den Typ PianoGruppe{Pianonote} definieren wie oben Akkorde, aber zunächst ohne Randbedingung über die Gleichheit der Einsatzzeiten. Dann könnte man durch Hinzufügung eines spezifischen Namens spezielle Gruppen auszeichnen, etwa:
Legatobogen(PianoGruppe), Staccato(PianoGruppe), Stimme(PianoGruppe), Part(PianoGruppe),...
je nach Bedeutung, die solche Gruppen haben.
Schliesslich kann man auch Listen von Akkorden betrachten (mit eckigen Klammern, um dies zu kennzeichnen),
deren Objekte dann so aussehen:
Akkordsequenz[Akk_1,Akk_2,...,Akk_n],
wobei Akk_1,Akk_2,...,Akk_n eine Folge von n Akkorde ist.
Die offene Frage wäre hier, ob man ein System finden kann, das alle Fälle erfasst, ohne ständig erweitert werden zu müssen. Wir werden dieses Problem später lösen im Rahmen der Theorie der Formen und Denotatoren...
Natürlich reicht es nicht, nur die symbolischen Daten zu kodieren, man muss auch die Hilfsdaten für die P-Transformation in die physikalische Ebene kodieren. Bild 35 zeigt dazu Max Regers Autograph zur Komposition An die Hoffnung op. 124. Reger hat die Performance-Zeichen rot geschrieben, um sie von den rein mentalen Zeichen zu unterscheiden.

Die Bedeutung dieser Zeichen ist im Text nicht eindeutig gegeben und muss durch zusätzliche Kompetenz "paratextuell" erfüllt werden. ZB: drei crescendi hintereinander ausgehend vom mf -Bereich. Wo ist man in der Lautstärke?
Die Performance-Abbildung zu bestimmen, ist ein aktueller und schwieriger Forschungsgegenstand der Performance-Forschung, wir werden darüber noch kurz sprechen im Rahmen der Diskussion der RUBATO-Software-Plattform.
Sowohl bei Komposition als auch bei Analyse werden Prozesse im musikalischen Zeichensystem benutzt, die man als syntagmatisch oder paradigmatisch charakterisieren kann.
Bei paradigmatischen Prozessen muss man zwei Typen unterscheiden, was die Etymologie para~nahe/bei und deigma~Verweis angibt. Erstere Wurzel (para) meint topologische Nachbarschaft, Verformung, Umgebung. Die zweite (deigma) meint Verweis, Transformation in etwas anderes. Wir geben anschliessend zu jedem Subtypus entsprechende Beispiele. Wesentlich ist hier, dass diese Prozesse nicht primär das Syntagma betreffen, sondern Verwandtschaften, Assoziationen erzeugen oder beschreiben, die im Syntagma u. U. weit auseinanderliegende Objekte betreffen.
| PARA: Deformationen und Variationen |
|---|
Diese Verfahren werden ganz prominent auch in Musiksoftware (Sequenzer, Kompositionssoftware) verwendet.
| DEIGMA: Transformationen und Symmetrien |
|---|
Vorbemerkung: Unter Transformationen verstehen wir Abbildungen, die sich durch Verschiebungen und lineare Transformationen zusammensetzen. Symmetrien sind umkehrbare Transformationen. Wir werden aber diese Begriffe nicht weiter verfolgen, sondern nur bekannte Beispiele diskutieren, um die Mathematik hier nicht zu strapazieren!
Hier werden also die assoziierten Objekte nicht durch Nachbarschaft oder Æhnlichkeit ermittelt, sondern als Resultat eines spezifischen Zeigens durch ein Werkzeug: die Transformation oder Symmetrie.
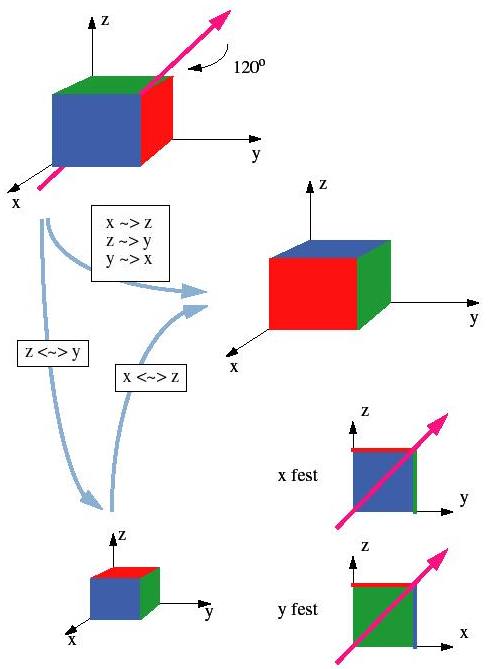
Bild 36 zeigt ein Beispiel, wie man eine 3D-Drehung von 120 Grad um die Körperdiagonale in 2D-Transformationen (Spiegelungen in unserem Fall) zerlegen kann. Zuerst vertauscht man nur die x und y Achsen (und vergisst momentan die z-Achse) und dann vertauscht man die x- und z-Achsen (und vergisst momentan die y-Achse).
| WEITER |